windows下Nginx反向代理服务器安装与配置

感谢慕课网Geely老师的讲解，本人将Nginx进行如下的总结。

Nginx是一款轻量级的Web服务器，也是一款反向代理服务器，其主要特点：高稳定, 高性能,资源占用少功能丰富,模块化结构 支持热部署。

主要作用：

• 可直接支持Rails和PHP程序
• 可作为Http反向代理工具
• 作为负载均衡的服务器
• 作为邮箱代理服务器
• 帮助实现前端动静分离

Ngin下载地址（http://nginx.org/download/）

nginx.conf文件配置

下载解压后打开conf下面的nginx.conf配置文件，在配置文件中我们通过“include vhost/*.conf;“ 嵌入其他配置文件，部分电脑可能会出现端口被占用的情况，在这里我们没有终止被占用的进程，而是改变将默认的80端口改成了81。

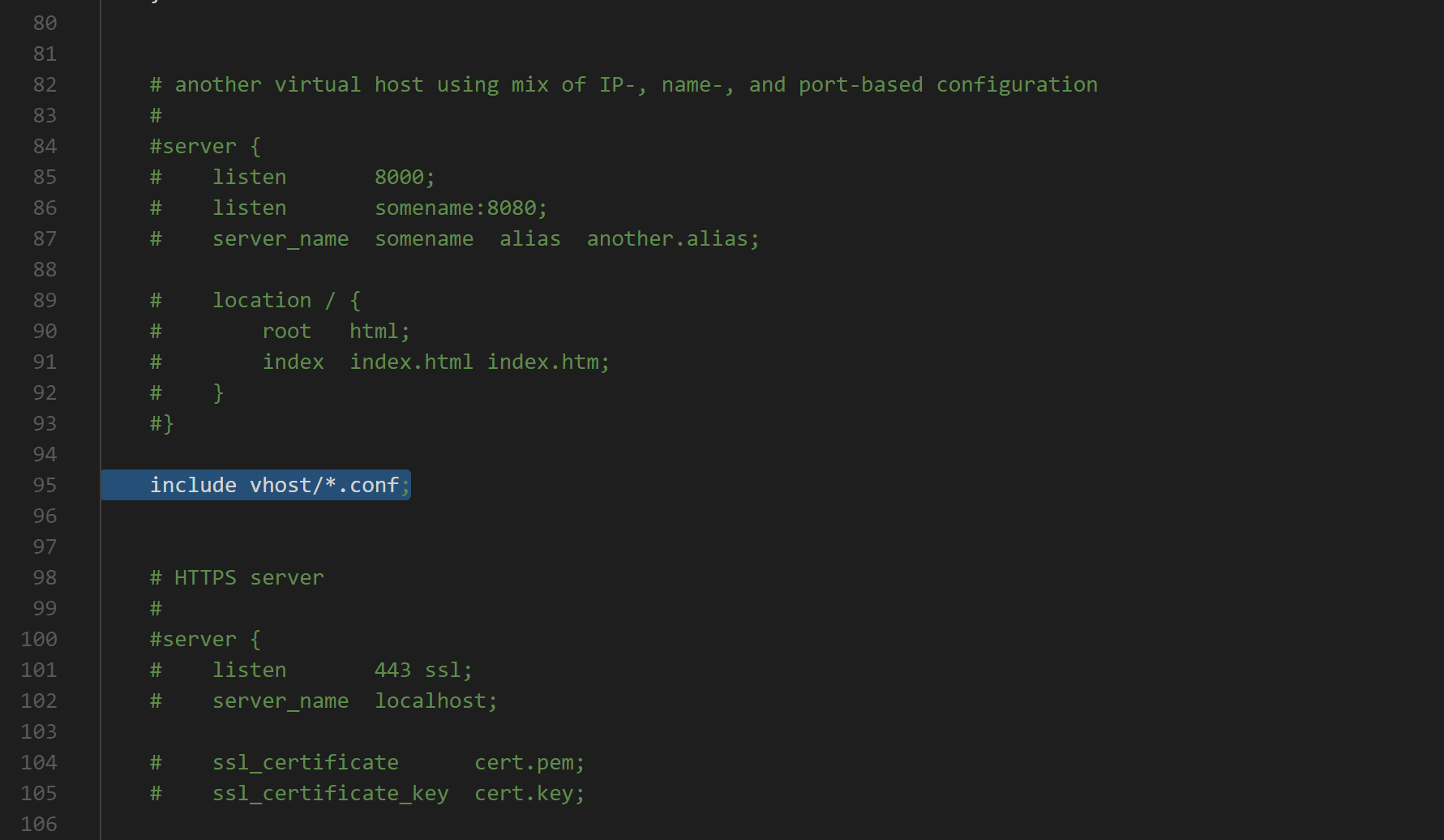
 配置vhost文件 

在conf目录下新建一个vhost文件夹，并在vhost下新建下面两个后缀名为conf的下面两个文件，image.imooc.com.conf是转发指向目录的，tomcat.imooc.com.conf是指向端口的。

server {
    listen 81;
    autoindex on;
    server_name image.imooc.com;
    access_log c:/access.log combined;
    index index.html index.htm index.jsp index.php;
    #error_page 404 /404.html;
    if ( $query_string ~* ".*[\;'\<\>].*" ){
        return 404;
    }

    location ~ /(mmall_fe|mmall_admin_fe)/dist/view/* {
        deny all;
    }

    location / {
        root D:\ftpfile;
        add_header Access-Control-Allow-Origin *;
    }
}

image.imooc.com.conf

server {
    listen 81;
    autoindex on;
    server_name tomcat.imooc.com;
    access_log c:/access.log combined;
    index index.html index.htm index.jsp index.php;
    #error_page 404 /404.html;
    if ( $query_string ~* ".*[\;'\<\>].*" ){
        return 404;
    }
    location / {
        proxy_pass http://127.0.0.1:8080;
        add_header Access-Control-Allow-Origin *;
    }
}

tomcat.imooc.com.conf

listen-->需要监听的端口

autoindex -->是否自动创建索引

server_name -->需要监听的服务名称

localtion-->配置需要转发端口或目录

配置虚拟域名

没钱购买域名的小伙伴们可以打开下面的目录修改window的hosts文件

C:\Windows\System32\drivers\etc

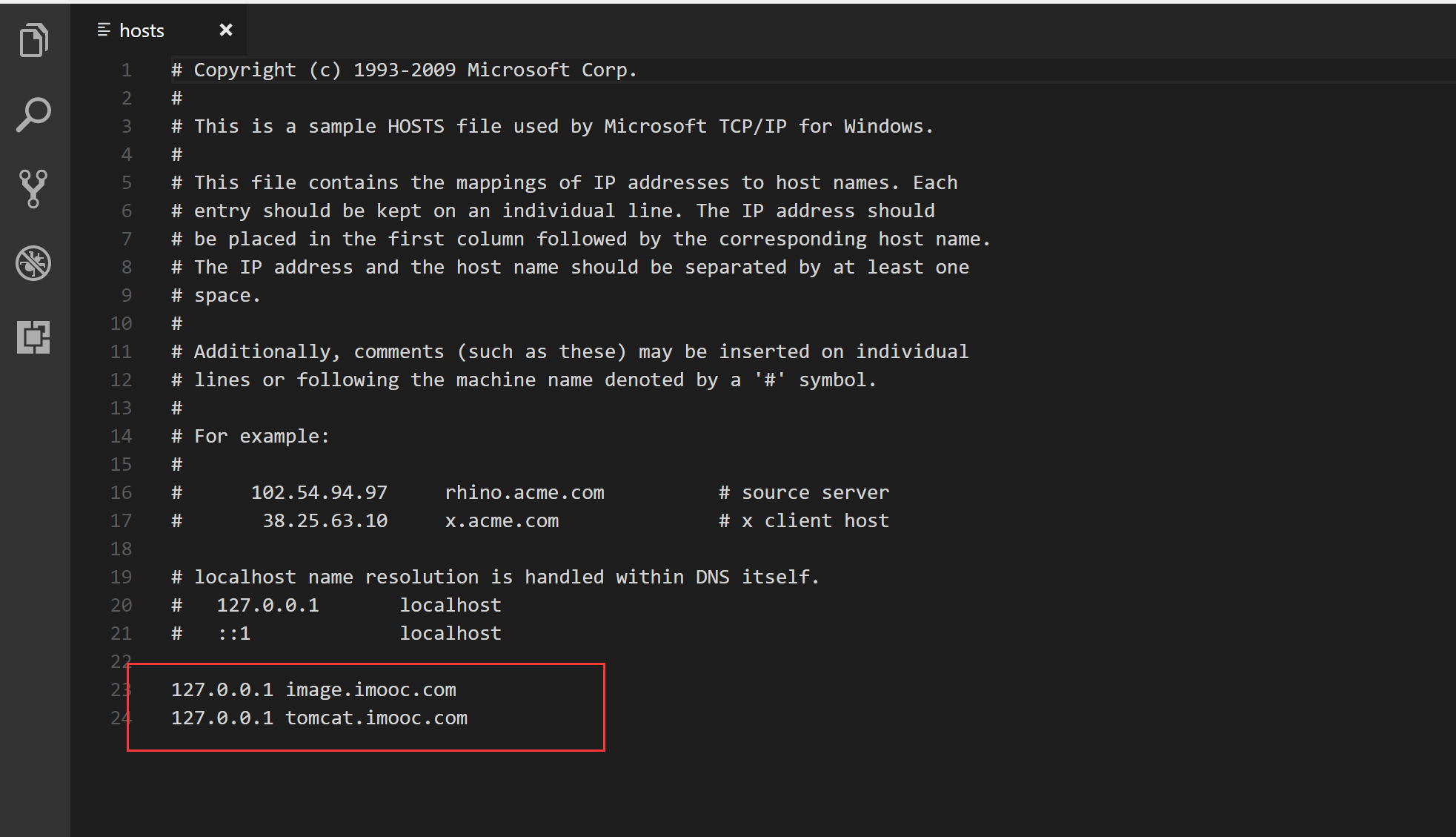
然后点击启动我们的Nginx，由于Nginx可能配置有误导致，Nginx启动不了，这里我们推荐使用CMD命令去找到并执行下nginx.exe文件，如过发生错误有助于我们很快的找到原因。如果没有问题，这时候在进程里我们可以找到我们Nginx的进程。

在这里我们事先启动了tomcat服务，与ftp文件服务器。通过访问tomcat.imooc.com:81 和 image.imooc.com:81两个地址，我们分别访问到了tomcat服务器的欢迎页和ftp文件服务器的目录

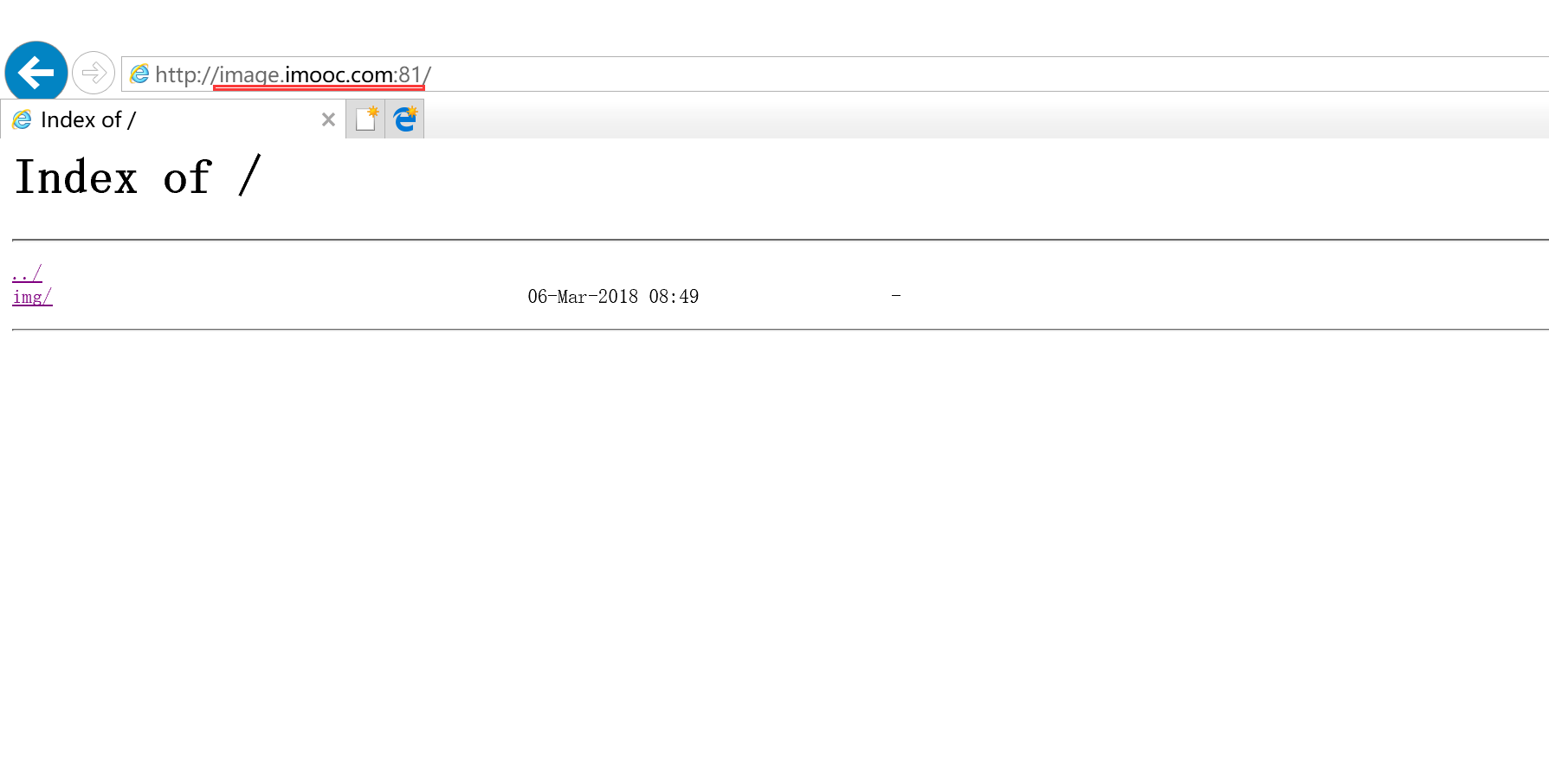
在这里nginx的配置就差不多了，如果我们使用的是默认的80端口的话，就可以直接把这里的端口号去掉。有兴趣的小伙伴可以换成自己域名去尝试下，有什么不够详细的地方，欢迎大家补充下。