leadcode的Hot100系列--78. 子集--回溯

上一篇说了使用位运算来进行子集输出，这里使用回溯的方法来进行排序。

回溯的思想，我的理解就是：

把解的所有情况转换为树或者图，然后用深度优先的原则来对所有的情况进行遍历解析。

当然，因为问题中会包涵这各种各样的限制条件，我们可以用这些限制条件去减少遍历的分支。

其实，比较著名的就是0-1背包问题，这个背包问题之后再说，这里先看排列组合。

假设我们的数组为[6,7,8]，依然使用0来表示当前数字不存在，用1来表示当前数字存在，我们就可以画出这样一个树：

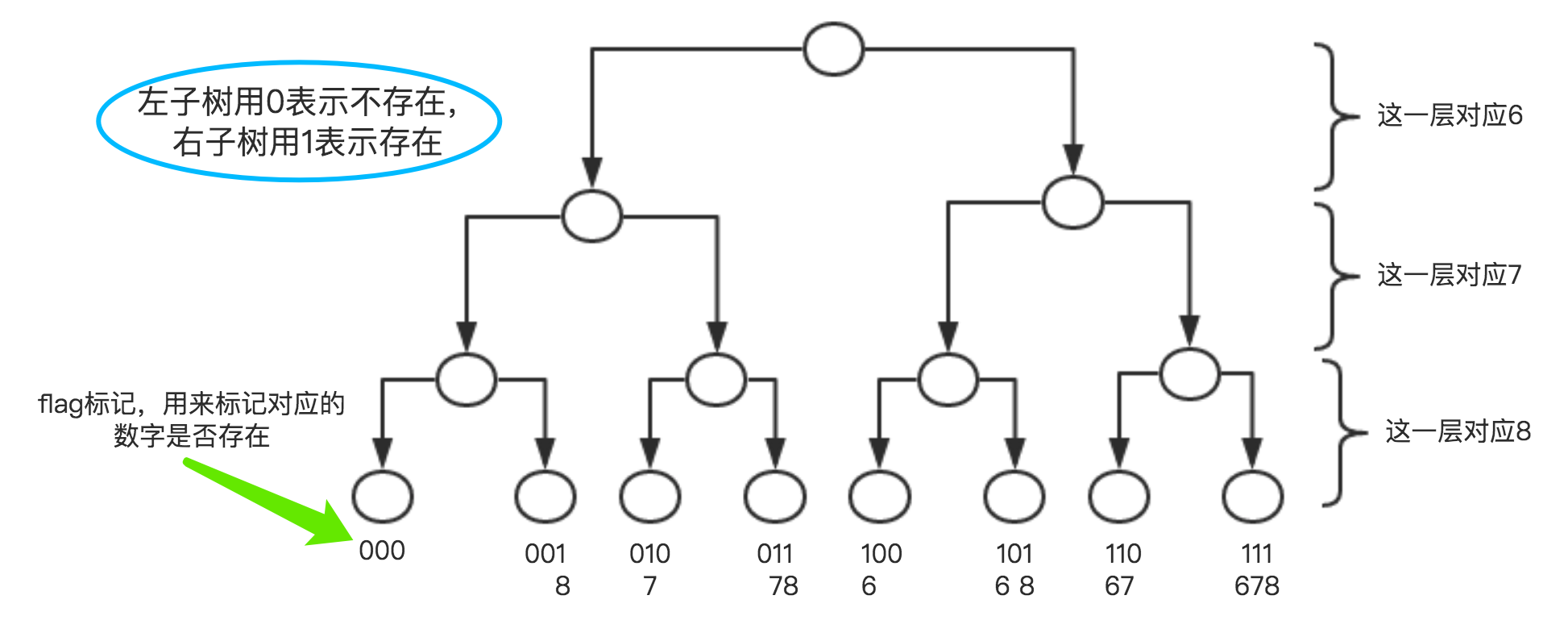
这里使用递归来生成对应的flag标记，重点是backtrack函数:

#include <stdio.h>

int x[] = {6,7,8};   // 需要排列的数组
int y[] = {0,0,0};   // 存放flag标记
int level = 3;       // 有3个数字需要进行排列，对应的就需要排3层

void show()
{
    for (int i=0; i<level; i++)
    {
        printf("flag : %d ", y[i]);
    }
    printf("\n");
}

void backtrack (int t)
{
    if (t == level)   // 当遍历深度等于level的时候，说明遍历完成，得到一组完整的flag标记
        show();
    else
        for (int i=0;i<=1;i++)   // 这里先生成0标记，再生成1标记
        {
            y[t]=i;            //  记录当前层是否存在，0存在，1不存在
            backtrack(t+1);   // 递归遍历下一层，这里可以根据题目限制来判断是否需要继续下一层的遍历，可以减少遍历次数
        }
}

int main(void)
{
    backtrack(0);
    return 0;
}

输出结果为：
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

回溯的基本就那么一个思想，那限制条件怎么用呢？

比如，我有10元钱，这里有三个物品，价格分别是8元，5元，2元，10元，

问，这10元钱可以有哪些买法？

这里存在的一个限制就是：总数不能超过10。

#include <stdio.h>

#define TOTAL 10  // 总数最多为10

int x[] = {8,5,2,10};  // 价格
int y[] = {0,0,0,0};
int level = 4;

void show()
{
    int n=0;
    for (int i=0; i<level; i++)   // 计算总价格是否超过10
    {
        n += y[i] * x[i];
    }
    if (TOTAL < n)
    {
        return;
    }
    for (int i=0; i<level; i++)   // 这里直接打印符合条件的价格
    {
        printf("%d ", y[i]*x[i]);
    }
    printf("\n");
}

void backtrack (int t)
{
    if (t == level)
        show();
    else
        for (int i=0;i<=1;i++)
        {
            y[t]=i;
            int n = 0;
            for (int j=0; j<t; j++)  // 这里先计算一下当前价格是多少
            {
                n = y[j] * x[j];
            }
            if (TOTAL > n)       // 如果当前价格已经超了，就不需要再递归下一层(因为不论下一层是否存在，总价格必然会超)，否则继续递归
                backtrack(t+1);
        }
}

int main()
{
    backtrack(0);
    return 0;
}
结果为：
0 0 0 0
0 0 0 10
0 0 2 0
0 5 0 0
0 5 2 0
8 0 0 0
8 0 2 0