奇异值分解（SVD）

　　首先说明一下特征值：设A是n阶方阵，如果存在 λ 和n维非零向量X，使 AX = λX ，则 λ 称为方阵A的一个特征值，X为方阵A对应于或属于特征值 λ 的一个特征向量。

　　AX = λX 的过程是一个从矩阵乘法到数乘操作的过程。数乘的实质是对向量X进行缩放，缩放因子为λ ，缩放只改变大小，不改变方向。找到特征值和特征向量的过程称为特征值分解，可以利用解线性方程组(λE-A)X=0 来完成。对应于不同特征值的特征向量线性无关，如果原矩阵A是对称矩阵，对应于不同特征值的特征向量必定正交 。

　　如果得到了N阶对称矩阵A的N个特征值，且N个特征值均不同，那么特征向量必定正交，就可以经过标准化后（是否需要，如何做？存疑？直接除以长度么？），作为A的标准正交基。将A向N个基上投影，投影长度=特征值绝对值，特征值越大，表示了矩阵在对应的特征向量上的方差越大，功率越大，信息量越多。因此，特征值分解得到了特征值和特征向量，特征值的大小表示了对应的特征有多重要，特征向量的方向表示了特征的属性。

　　既然特征值越大的方向上包含了越多的信息，就可以在特征值分解后，只保留特征值较大的方向对应的数据，删除小特征值对应方向的数据，保证了数据量减少，而有用信息基本不变，这就是PCA的思想。

　　（有一个疑问：只有对称阵的特征值不同才能保证特征向量彼此正交，如果特征值相同，线性无关无法保证，如何找正交基呢？）

　　注意：特征值分解要求A是方阵，如果A不是方阵，而是一个1920x1080的灰度图构成的矩阵，无法找特征值，此时可以找奇异值。

　　

　　奇异值：矩阵A的大小为mxn，奇异值分解将矩阵分解成若干个秩一矩阵之和，即

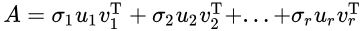
每个都是奇异值，按照从大到小的顺序排列，u和v分别表示列向量，uv' 是秩为1的矩阵，（ 可以利用 R(A)+R(B)-n <= R(AB) <= min{R(A),R(B)} 得到R(uv')=1）。只保留较大的奇异值对应的数据，同样可以达到降维的效果。下面是对一张图片进行的实验。

Matlab代码如下：

 clear,clc;
 close all;

 imgorigin = imread('saoirse.jpg');
 imgray = double(rgb2gray(imgorigin));
 subplot();imshow(imgray,[]);title('original-gray');
 [m,n] = size(imgray);
 [U,S,V] = svd(imgray);
 %返回与imgray同大小的对角矩阵S,两个矩阵U和V,且满足imgray=U*S*V'
 %若imgray大小为m×n,则U为m×m矩阵,V为n×n矩阵.S为m×n矩阵,奇异值在S的对角线上

 decomp = U(:,:)*S(:,)*V(:,)';
 subplot();imshow(decomp,[]);title('svd-前1个特征');

 decomp = U(:,:)*S(:,:)*V(:,:)';
 subplot();imshow(decomp,[]);title('svd-前5个特征');

 decomp = U(:,:)*S(:,:)*V(:,:)';
 subplot();imshow(decomp,[]);title('svd-前10个特征');

 decomp = U(:,:)*S(:,:)*V(:,:)';
 subplot();imshow(decomp,[]);title('svd-前50个特征');

 decomp = U(:,:)*S(:,:)*V(:,:)';
 subplot();imshow(decomp,[]);title('svd-前80个特征')

 decomp = U(:,:)*S(:,:)*V(:,:)';
 subplot();imshow(decomp,[]);title('svd-前150个特征');

 decomp = U(:,:)*S(:,:)*V(:,:)';
 subplot();imshow(decomp,[]);title('svd-前220个特征');

 decomp = U(:,:)*S(:,:)*V(:,:)';
 subplot();imshow(decomp,[]);title('svd-前282个特征');

参考：

1. https://blog.csdn.net/index20001/article/details/73501632

2. https://www.zhihu.com/question/22237507

3. 线性代数与空间解析几何-郑宝东