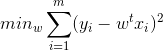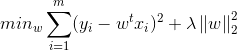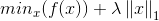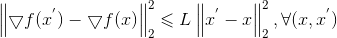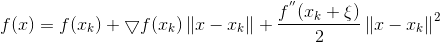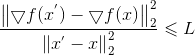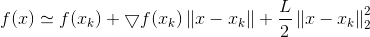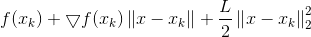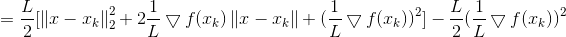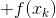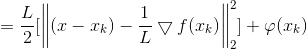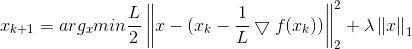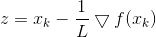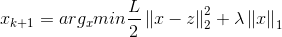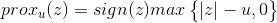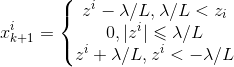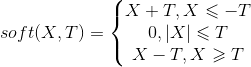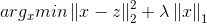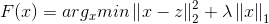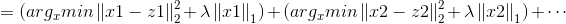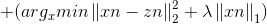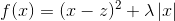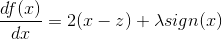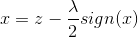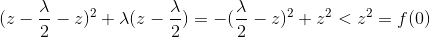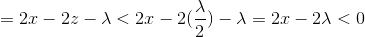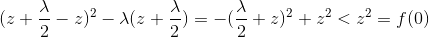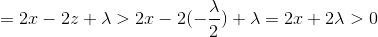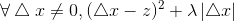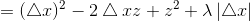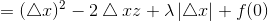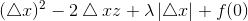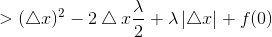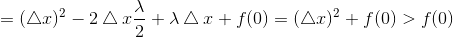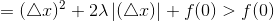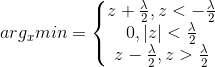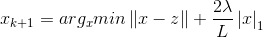LASSO回归与L1正则化 西瓜书
1.结构风险与经验风险
在支持向量机部分,我们接触到松弛变量,正则化因子以及最优化函数,在朴素贝叶斯分类,决策树我们也遇到类似的函数优化问题。其实这就是结构风险和经验风险两种模型选择策略,经验风险负责最小化误差,使得模型尽可能的拟合数据,而结构风险则负责规则化参数,使得参数的形式尽量简洁,从而达到防止过拟合的作用.所以针对常见模型,我们都有下式:
第一项经验风险L(yi,f(xi,w))衡量真实值与预测值之间的误差,第二项结构风险Ω(w)规则化项使得模型尽可能简单.而第二项Ω(w)一般是模型复杂度的单调函数,模型越复杂,则规则化项的值越大,这里常引入范数作为规则化项,这也就引入了我们常见的L0范数,L1范数以及L2范数.
2.L0范数,L1范数,L2范数与LASSO回归,岭回归
1)广义定义
L0范数 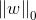
L1范数 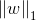
L2范数 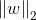
L0,L1范数可以实现稀疏化,而L1系数因为有比L0更好的特性而被广泛应用,L2范数在回归里就是岭回归,也叫均值衰减,常用于解决过拟合,通过对向量各元素平方和再求平方根,使得L2范数最小,从而使得参数W的各个元素都接近于0,与L1范数不同,L2范数规划后w的值会接近于0但不到0,而L1范数规范后则可能令w的一些值为0,所以L1范数规范在特征选择中经常用到,而L2范数在参数规则化时经常用到.在回归模型中,通过添加L1,L2范数引入正则化项,便得到了LASSO回归和岭回归:
2)回归模型
常见线性模型回归:
LASSOO回归:
岭回归:
3.嵌入式选择与LASSO回归
这里主要针对西瓜书第11节的内容,对近端梯度下降PGD法解决L1正则化问题进行讨论.
1)优化目标
令▽表示微分算子,对优化目标:
若f(x)可导,且▽f 满足L-Lipschitz(利普希茨连续条件),即存在常数L>0使得:
2)泰勒展开
则在Xk处我们可以泰勒展开:
上式是严格相等,由L-Lipschitz条件我们可以看到:
这里给出了一个L的下界,且下界的形式与二阶导函数形式类似,从而泰勒展开式的二阶导便通过L替代,从而严格不等也变成了近似:
3)简化泰勒展开式
接下来我们化简上式:
其中φ(xk)是与x无关的const常数.
4)简化优化问题
这里若通过梯度下降法对f(x)进行最小化,则每一步下降迭代实际上等价于最小化二次函数f(x),从而推广到我们最上面的优化目标,类似的可以得到每一步的迭代公式:
令
则我们可以先计算z,再求解优化问题:
5)求解
令xi为x的第i个分量,将上式展开可以看到没有xixj(x≠j)的项,即x的各分量互不影响,所以优化目标有闭式解.这里对于上述优化问题求解需要用到Soft Thresholding软阈值函数,其解为:
对于本例,带入求解即得:
因此,PGD能使LASSO和其他基于L1范数最小化的方法得以快速求解.
4.Soft Thresholding软阈值函数证明
1)软阈值函数
上式求解用到了软阈值函数,下面对软阈值函数的解进行求证,从而更好理解上述求解过程.
先看一下软阈值函数:
2)证明
Proof:
对于优化问题:
此处X,Z均为n维向量.
展开目标函数:
从而优化问题变为求解N个独立的函数:
这是我们常见的二次函数,对其求导:
令导数为0:
看到两边都有x,所以我们要对上述情况进行讨论:
A.z>λ/2时
假设 x<0 , 所以 sign(x)=-1 ,但 z-λ/2sign(x)>0 ,所以矛盾.
假设 x>0 ,所以 sign(x) = 1,z-λ/2sign(x)>0,所以极小值在x>0 取得1.
此时极小值小于f(0):
再看x<0,
所以f(x)在负无穷到0单调递减,所以最小值在z-λ/2处取得.
B.z<-λ/2时
假设 x<0 , 所以 sign(x)=-1 ,z-λ/2sign(x)<0 ,所以极值点在 x<0 处取得.
假设 x>0 ,所以 sign(x) = 1,z-λ/2sign(x)<0,所以矛盾.
此时极值小于f(0):
再看 x>0 ,
所以f(x)在0到正无穷单调递增,所以最小值在z+λ/2处取得.
C.λ/2<z<λ/2时
假设 x<0 , 所以 sign(x)=-1 ,z-λ/2sign(x)>0 ,所以矛盾.
假设 x>0 ,所以 sign(x) = 1,z-λ/2sign(x)<0,所以矛盾.
所以x>0,x<0均不满足条件.
所以有:
当△x>0时,由条件z<λ/2:
当△x<0时,由条件z<λ/2:
所以在0处取极小值,同时也是最小值.
综合以上三种情况:
3)对应西瓜书的L1正则化与LASSO回归
这里的解对应的优化问题是:
而我们PGD优化的问题是:
对上式同乘2/L不影响极值点位置的选取,所以我们的PGD优化问题变成:
带入综合三种情况的到的最终解:
西瓜书上11.14也就得证了~
总结:
终于看完了西瓜书11章特征选择与稀疏学习,发现从头至尾都在提到用LASSO解决问题,所以就结合第六章的正则化和之前的模型评价,对正则化范数以及LASSO重新认识了一下,书中解决LASSO的大致方法就是通过利普希茨连续条件得到L,带入到优化函数中对函数简化变形,简易优化函数,然后通过软阈值函数得到最后的解.LASSO大致就是这些了,有问题欢迎大家交流~
LASSO回归与L1正则化 西瓜书的更多相关文章
- 机器学习之五 正则化的线性回归-岭回归与Lasso回归
机器学习之五 正则化的线性回归-岭回归与Lasso回归 注:正则化是用来防止过拟合的方法.在最开始学习机器学习的课程时,只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数.但是一直也无法对其基 ...
- L1正则化和L2正则化
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择 L2正则化可以防止模型过拟合(overfitting):一定程度上,L1也可以防止过拟合 一.L1正则化 1.L1正则化 需注意, ...
- Lasso回归算法: 坐标轴下降法与最小角回归法小结
前面的文章对线性回归做了一个小结,文章在这: 线性回归原理小结.里面对线程回归的正则化也做了一个初步的介绍.提到了线程回归的L2正则化-Ridge回归,以及线程回归的L1正则化-Lasso回归.但是对 ...
- 机器学习--Lasso回归和岭回归
之前我们介绍了多元线性回归的原理, 又通过一个案例对多元线性回归模型进一步了解, 其中谈到自变量之间存在高度相关, 容易产生多重共线性问题, 对于多重共线性问题的解决方法有: 删除自变量, 改变数据形 ...
- 岭回归和Lasso回归以及norm1和norm2
norm代表的是距离,两个向量的距离:下图代表的就是p-norm,其实是对向量里面元素的一种运算: 最简单的距离计算(规范)是欧式距离(Euclidean distance),两点间距离是如下来算的, ...
- 【机器学习】正则化的线性回归 —— 岭回归与Lasso回归
注:正则化是用来防止过拟合的方法.在最开始学习机器学习的课程时,只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数.但是一直也无法对其基本原理有一个透彻.直观的理解.直到最近再次接触到这个概念 ...
- 通俗易懂--岭回归(L2)、lasso回归(L1)、ElasticNet讲解(算法+案例)
1.L2正则化(岭回归) 1.1问题 想要理解什么是正则化,首先我们先来了解上图的方程式.当训练的特征和数据很少时,往往会造成欠拟合的情况,对应的是左边的坐标:而我们想要达到的目的往往是中间的坐标,适 ...
- 【深度学习】L1正则化和L2正则化
在机器学习中,我们非常关心模型的预测能力,即模型在新数据上的表现,而不希望过拟合现象的的发生,我们通常使用正则化(regularization)技术来防止过拟合情况.正则化是机器学习中通过显式的控制模 ...
- 岭回归和lasso回归(转)
回归和分类是机器学习算法所要解决的两个主要问题.分类大家都知道,模型的输出值是离散值,对应着相应的类别,通常的简单分类问题模型输出值是二值的,也就是二分类问题.但是回归就稍微复杂一些,回归模型的输出值 ...
随机推荐
- Flutter安装
下载右边的安装包以获取最新版本 stable 的 Flutter SDK 将压缩包解压,然后把其中的 flutter 目录整个放在你预想的 Flutter SDK 安装目录中(比如 C:\src\fl ...
- linux 后台 运行
但是如果终端关闭的话,程序也会终止,那么就要涉及到linux的一个十分强大的命令:screen. 按照我个人的理解,这个命令就是能够在linux中创造出多个终端,在已有的窗口内部再创造更多的窗口,结合 ...
- 【java中的final关键字】
转自:https://www.cnblogs.com/xiaoxi/p/6392154.html 一.final关键字的基本用法 在Java中,final关键字可以用来修饰类.方法和变量(包括成员变量 ...
- 周志华-机器学习西瓜书-第三章习题3.5 LDA
本文为周志华机器学习西瓜书第三章课后习题3.5答案,编程实现线性判别分析LDA,数据集为书本第89页的数据 首先介绍LDA算法流程: LDA的一个手工计算数学实例: 课后习题的代码: # coding ...
- epoll简介 与 UDP server的实现
Abstractepoll是Linux内核为处理大批量句柄而作了改进的poll,是Linux下多路复用IO接口select/poll的增强版本,它能显著减少程序在大量并发连接中只有少量活跃的情况下的系 ...
- fastjson在将Map<Integer, String>转换成JSON字符串时,出现中文乱码问题
fastjson在将Map<Integer, String>转换成JSON字符串时,出现中文乱码问题. 先记下这个坑,改天在看看是怎么导致的,暂时通过避免使用Integer作为键(使用St ...
- dubbo 支持的9种协议
转: dubbo 支持的9种协议 文章目录 一.9种协议 1.dubbo 协议 (默认) 2.rmi 协议 3.hessian 协议 4.htt ...
- Qt编写安防视频监控系统12-异形布局
一.前言 视频监控系统中,除了常规的1画面.4画面.9画面.16画面以外,还有几个布局比较另类,比如6画面.8画面.13画面,有些通道需要占据不同的行列,4画面.9画面.16画面都是非常对称的布局,行 ...
- python3 高级编程(二) 动态给类添加方法功能
class Student(object): pass 给实例绑定一个属性: >>> s = Student() >>> s.name = 'Michael' # ...
- 免费申请https
https://blog.csdn.net/MariaOzawa/article/details/81877756 实测有效