HDU - 1045 Fire Net (二分图最大匹配-匈牙利算法）

匈牙利算法简介

个人认为这个算法是一种贪心+暴力的算法，对于二分图的两部X和Y，记x为X部一点，y为Y部一点，我们枚举X的每个点x，如果Y部存在匹配的点y并且y没有被其他的x匹配，那就直接匹配；如果Y中已经没有可以和x匹配的点(包括可以匹配的点已经被其他的x匹配)，那就让已经匹配的y的原配x'寻找其他可以匹配的y’，并将y和x匹配，最后，统计出匹配的对数

（详细了解的话，可以看看这位的博客：https://blog.csdn.net/sunny_hun/article/details/80627351）

题意

在一个n*n的网格中，存在一些墙壁，用'X‘表示，我们需要摆放blockhouse，由于每个blockhouse会向四周发射子弹，所以任意两个blockhouse不能在一条直线上，除非他们之间有墙壁分隔，问在给定的网格中，最多可以摆放多少个blockhouse

解题思路

（一开始我想用深搜暴力写的，过了样例，但是WA了，觉得自己的暴力写法没什么问题的，但是一直过不了，就只能放弃暴力了）

注意到如果我们在每个点放置了blockhouse，那么这个blockhouse向四个方向延申至墙壁或者边界，这个blockhouse可以视作是由一段连续的横区间和纵区间的交点，如下图所示：

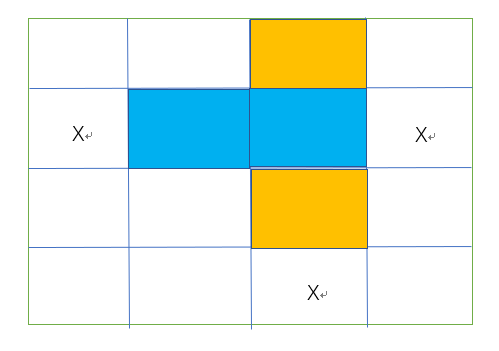
因此，我们发现，连续的纵横区间的交点形成一个blockhouse，并使得这两个区间都无法放置其他的blockhouse，由此看出这是一个求二分图最大匹配的问题

我们将连续的纵区间当作一个点，作为X部，将练习的横区间当作一个点，作为Y部，对于相交的横纵区间，我们由纵区间代表的点向横坐标代表的点建边，构建二分图

随后我们可以通过将二分图转化使用最大流求解，也可以用匈牙利算法求解，由于Dinic算法代码量冗长，这里就采用了匈牙利算法求解

代码区

#include<iostream>

#include<cstdio>

#include<algorithm>

#include<cstring>

#include<queue>

#include<string>

#include<fstream>

#include<vector>

#include<stack>

#include <map>

#include <iomanip>

#define bug cout << "**********" << endl

#define show(x, y) cout<<"["<<x<<","<<y<<"] "

#define LOCAL = 1;

using namespace std;

typedef long long ll;

const int inf = 1e7 + ;

const ll mod = 1e9 + ;

const int Max = 1e6 + ;

const int Max2 = 3e2 + ;

int n;

char mp[][];

int row_id[][], col_id[][], cnt_row, cnt_col;    //记录每个点所处的行、列编号

bool edge[][], vis[];                            //代表是否配对以及是否已经占用

int match[];

bool dfs(int x)

{

    for (int i = ; i < cnt_col; i++)

    {

        if (edge[x][i] && !vis[i])

            //used表示曾试图改变i的匹配对象，但是没有成功的话（used[i]= true)，所以就无需继续

        {

            vis[i] = true;

            if (match[i] == - || dfs(match[i]))    //i没有匹配对象，或者i原来的匹配对象还可以和其他的匹配

            {

                match[i] = x;

                return true;

            }

        }

    }

    return false;

}

int solve()

{

    int res = ;

    memset(match, -, sizeof(match));

    for (int i = ; i < cnt_row; i++)

    {

        memset(vis, , sizeof(vis));

        if (dfs(i))

            res++;

    }

    return res;

}

int main()

{

#ifdef LOCAL

    //    freopen("input.txt", "r", stdin);

    //    freopen("output.txt", "w", stdout);

#endif

    while (scanf("%d", &n) != EOF && n)

    {

        cnt_row = cnt_col = ;

        memset(edge, , sizeof(edge));

        for (int i = ; i <= n; i++)

        {

            scanf("%s", mp[i] + );

        }

        for (int i = ; i <= n; i++)

        {

            for (int j = ; j <= n; j++)

            {

                if (mp[i][j] == '.')

                {

                    int u = , v = ;

                    if (j ==  || mp[i][j - ] == 'X')

                        u = cnt_row++;

                    else

                        u = row_id[i][j - ];

                    if (i ==  || mp[i - ][j] == 'X')

                        v = cnt_col++;

                    else

                        v = col_id[i - ][j];

                    edge[u][v] = true;

                    row_id[i][j] = u;

                    col_id[i][j] = v;

                }

            }

        }

        printf("%d\n", solve());

    }

    return ;

}

题外延申

匈牙利算法复杂度O(VE)

最小点覆盖=最大匹配数

最小边覆盖=左右点数-最大匹配数

最小路径覆盖=点数-最大匹配数

最大独立集=点数-最大匹配数