C#实现有向无环图(DAG)拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序.

线性结构概念

总的来说，“线性结构”是一个有序数据元素的集合 线性结构满足以下特点：

1. 集合中必存在唯一“第一个元素”；
2. 集合中必存在唯一“最后一个元素”；
3. 除了最后一个元素，所有元素均有唯一“后继结点”；
4. 除了第一个元素，所有元素均有唯一“前趋结点”

和我们abp Module很像，第一个加载模块永远是其ABP核心模块,最后一个模块永远是我们的启动模块

举例

1.大学课程排序

大学课程的学习是有先后顺序的，C语言是基础，数据结构依赖于C语言，其它课程也有类似依赖关系。这样的一个课程安排是怎么实现的呢？

2.VS项目编译顺序

假设VS中有三个项目A,B，C，它们的关系如下。VS编译器是如何判断三个项目的编译顺序的呢？

A->B->C A引用B B引用C

A->B->C->A 提示循环引用

ABP的Module

ABP中的模块也是如此,不可循环引用相互依赖A->B B->A X

前面说到ABP中的第一个模块和最后一个模块是确定的。

呢么中间的是怎么排序的呢。其实用的是拓扑算法



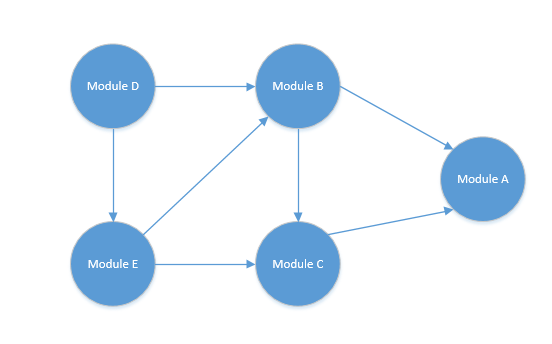
从图中可以得知:

1.A模块是最核心的，不依赖于其他任何模块

2.D依赖E和B,E依赖B和C，B依赖C和A，C依赖A

那么根据拓扑排序,应该如何排序呢？

1.从图中找一个没有前驱指向它的顶点

2.删除该顶点.以及该顶点的前驱

3.重复步骤 1 and 2 ,直到图中顶点为空 或者 找不到步骤1中这样的顶点 为止.

排序如下:



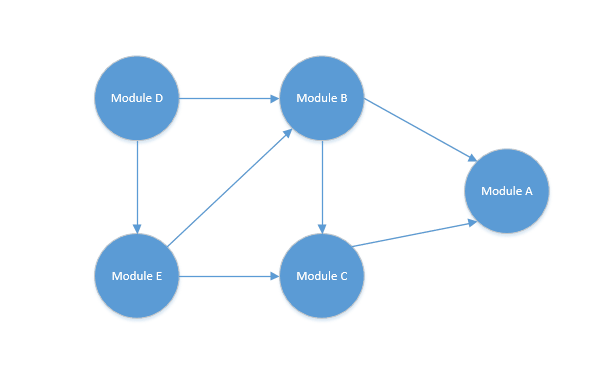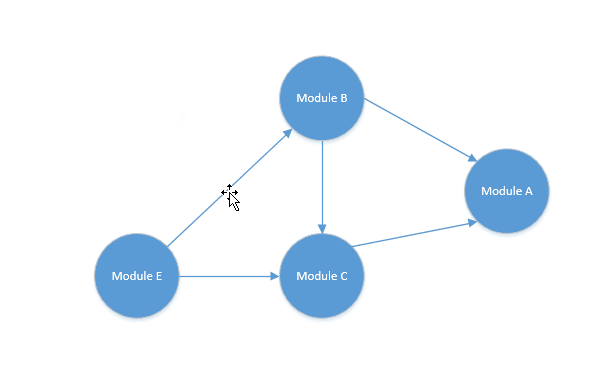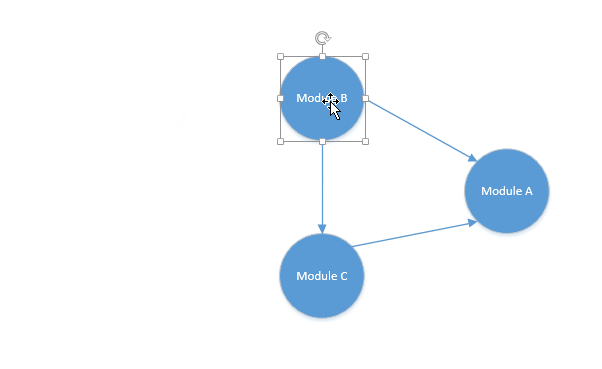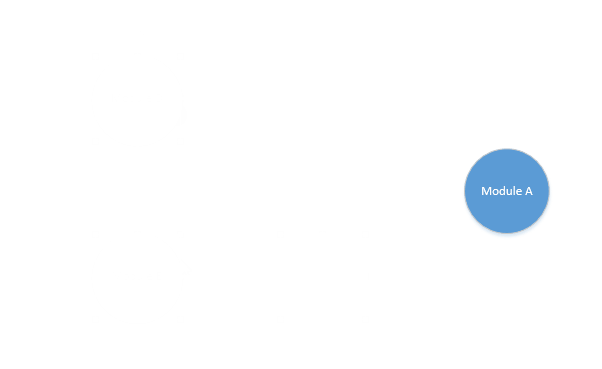
结果就是D->E->B->C->A 排完之后正好对应D依赖E和B,E依赖B和C，B依赖C和A，C依赖A

这个顺序在ABP的模块这看来是行不通的，需要在反转一次，最先加载A，才行。

C#实现深度优先搜索

有这样一个DAG图



如果对它进行排序的话,其实过程是这样的.

图中,顶点A是没有指向它的前驱的，所以从它开始访问



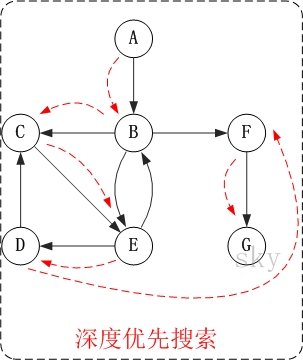
1.访问 A

2.访问 B

3.访问 C

在访问了 B 后应该是访问 B 的另外一个顶点，这里可以是随机的也可以是有序的，具体取决于你存储的序列顺序，这里先访问 C 。

4.访问 E

5.访问 D

这里访问 D 是因为 B 已经被访问过了，所以访问顶点 D 。

6.访问 F

因为顶点 C 已经被访问过，所以应该回溯访问顶点 B 的另一个有向边指向的顶点 F 。

7.访问 G

那么代码应该如何写呢?

source:需要排序的集合

getDepends:一个func委托，用于获取当前模块依赖的其他模块

方法内部维护了一个字典对象Visited 用于存储已经访问过的模块,key表示模块,value是一个bool，true时表示正在处理，false表示以及处理完成，

处理完成的模块会加入到sorted集合中

static List<T> MySort<T>(IEnumerable<T> source, Func<T, IEnumerable<T>> getDepends)
{
    // 访问过的路径
    Dictionary<T, bool> visited = new Dictionary<T, bool>();
    // 已经排过序的
    List<T> sorted = new List<T>();
    foreach (var item in source)
    {
        Visit<T>(item, getDepends, visited, sorted);
    }
    return sorted;
}

static void Visit<T>(T item, Func<T, IEnumerable<T>> getDepends, Dictionary<T, bool> visited, List<T> sorted)
{
    //已经访问过了
    if (visited.ContainsKey(item))
    {
        bool isVisit = visited[item];
        if (isVisit == true)
        {
            throw new Exception("循环引用");
        }
    }
    //未访问
    else
    {
        visited.Add(item, true);//true :正在访问 false:访问完成

        //获取所有依赖
        var depends = getDepends(item);
        foreach (var depend in depends)
        {
            Visit(depend, getDepends, visited, sorted);
        }

        //访问完成
        visited[item] = false;
        sorted.Add(item);
    }

}

完整demo github