《机器学习实战》PCA降维

---

注释：由于各方面原因，理论部分不做介绍，网上很多自行百度吧！

---

pca.py

 import numpy as np
 import matplotlib.pyplot as plt
 import math

 def  loadDataSet(filename, delin = '\t'):
     fr = open(filename)
     #读取分割存入数组
     stringArr = [line.strip().split(delin) for line in fr.readlines()]
     dataArr   = [list(map(float,line)) for line in stringArr]
     return np.mat(dataArr)
 def pca(dataMat, topNfeet = 9999999):
     meanVals = np.mean(dataMat,axis=0)#求取平均值
     meanRemoved = dataMat - meanVals
     covMat = np.cov(meanRemoved,rowvar=0)#方差
     eigVals, eigVects= np.linalg.eig(np.mat(covMat))#求解特征向量和特征值
     eigValInd = np.argsort(eigVals)#对特征值进行排序
     eigValInd = eigValInd[:-(topNfeet+1):-1]#最后的-1是防止越界的，当然你可以在前面加一个判断
     redEigVects = eigVects[:,eigValInd]
     lowDDataMat = meanRemoved*redEigVects #
     reconMat = (lowDDataMat * redEigVects.T) + meanVals
     return lowDDataMat, reconMat

main.py

 import PCA
 import matplotlib.pyplot as plt

 if __name__ == "__main__":

     dataMat = PCA.loadDataSet('testSet.txt')
     lowDMat, reconMat = PCA.pca(dataMat,1)
     fig = plt.figure()
     ax  = fig.add_subplot(111)
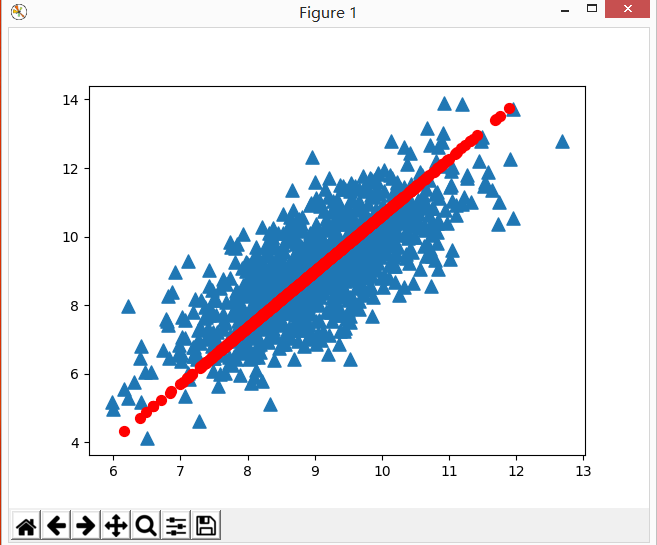
     ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],marker = '^',s=90)
     ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker = "o",s=50,c='red')
     plt.show()

对丢失的值进行替代：

 #零的数据都转化为平均值
 def replaceNanWithMean():
     dataMat = loadDataSet('secom.data',' ')
     numFeat = dataMat.shape[1]
     for i in range(numFeat):
         meanVal = np.mean(dataMat[np.nonzero(~np.isnan(dataMat[:,i].A))[0],i])
         dataMat[np.nonzero(np.isnan(dataMat[:,i].A))[0],i] = meanVal
     return dataMat