bzoj4842: [Neerc2016]Delight for a Cat

bzoj4842

这是一道网络流的题（大家都看出来了吧）

首先我们简化一下题目，选出最关键的部分（就是知道什么和要求什么，还有条件）

我们在这里把睡觉设为0，至少有t0时间在睡觉，把打隔膜设为1，至少t2时间在打隔膜（方便下面描述）

这样的话就转换成了一个序列问题 ，数列上的点可以选为0或1，第i个位置选0有si的收益，选1有ei的收益，长度为k的序列里至少有t0个0和t1个1。求如何填数才能令这个序列达的收益最大，输出最大收益和填数方案。

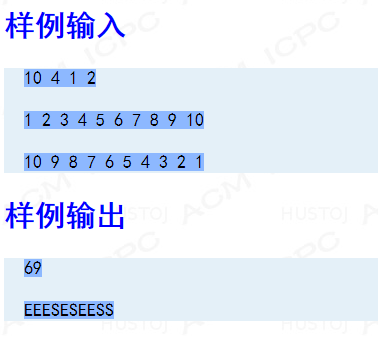样例就不用解释了吧，大家都懂。

假设所有点都选了0，操作由赋值0或1改为将哪些0变为1后更优，每一个0变为1后都有ei-si的收益，一个长度为k的区间内至少有t1个1，定为下界L=t1，至多有k-t0个1（至少有t0个0）定为上界U，（是有上下界的网络流的题！！不过正解不是那样）这样变换后可以试操作更简单。

既然是网络流的，我们考虑怎么建图，一看是一个序列，先把序列上的点依次连接起来S连向1，n连向T，中间的i连向i+1；

然后步入正题，看看本题应该怎么做，参考一下下图：

先只考虑有上界的问题

对于每个点i，我们将它像i+k号点连一条边，表示选了这个点（0改为1），将这一点的流量分走，分向下一个区间，剩下的流量就 -1  表示这个区间内能改的点的个数-1。

将S流向1 的边流量设定为上界U，这样可以保证每个k区间的流量都<=上界。这样就能控制住每个区间内最多分出去U的流量，就是说最多选上界个点；

再考虑下界，就是最少选L个1；也就是说要让这个区间内最少流出L的流量，那么剩下的流量最多就只能流U-L了。所以我们把每个区间末尾的那个边的流量定为U-L控制最多剩下多少流量。

（大家用各种优美姿势感性理解一下）

还有注意不要全开long long ;

不开long long会爆int ，全开会超时~~~这个东西卡了我一个小时。。

至于怎么输出方案，大家胡乱搞一下就好了。

 #include<iostream>
 #include<queue>
 #include<bit/stdc++.h>
 using namespace std;
 #define LL long long
 #define C continue
 #define B break
 #define MAXN 101000
 #define inf 100000007
 inline LL read()
 {
     LL x=,f=;
     char ch=getchar();
     while(ch>''||ch<''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }
 int n,k,t0,t1,S,T,lin[MAXN],t=;
 int v[MAXN],pre[MAXN],U,L,id[MAXN],S0;
 LL aa,d[MAXN],AKAKAKAK[MAXN],a[MAXN],ans=,sum;
 int incf[MAXN];
 struct adge{
     int y,ne,c,v;
 }e[*MAXN];
 void insert(int xx,int yy,int cc,int vv)
 {
     e[++t].y=yy;e[t].v=vv;e[t].c=cc;e[t].ne=lin[xx];lin[xx]=t;
     e[++t].y=xx;e[t].v=-vv;e[t].c=;e[t].ne=lin[yy];lin[yy]=t;
 }queue<int> q;
 bool SP_spfa(int st)
 {
     while(q.size())q.pop();
     memset(d,,sizeof(d));
     aa=d[];
     memset(v,,sizeof(v));
     q.push(st),d[st]=,v[st]=;
     incf[st]=(<<);
     while(q.size())
     {
         int x=q.front();
         q.pop();
         v[x]=;
         for(int i=lin[x];i;i=e[i].ne)
         {
             int y=e[i].y;
             if(d[y]>d[x]+e[i].v&&e[i].c)
             {
                 d[y]=d[x]+e[i].v;
                 incf[y]=min(incf[x],e[i].c);
                 pre[y]=i;
                 if(!v[y])
                 {
                     v[y]=;
                     q.push(y);
                 }
             }
         }
     }
     if(d[T]==aa)    return ;
     return ;
 }
 void Update()
 {
     int x=T;
     while(x!=S)
     {
         int i=pre[x];
         e[i].c-=incf[T];
         e[i^].c+=incf[T];
         x=e[i^].y;
     }
     ans+=(LL)d[T]*incf[T];
 }
 int main()
 {
     //freopen("www.in","r",stdin);
     //freopen("www.out","w",stdout);
     n=read(),k=read(),t0=read(),t1=read();
     for(int i=;i<=n;++i)    AKAKAKAK[i]=read(),sum+=AKAKAKAK[i];
     for(int i=;i<=n;++i)    a[i]=read()-AKAKAKAK[i];
     S=,T=n+;U=k-t0;L=t1;S0=n+;
     insert(S,S0,U,);
     for(int i=;i<=n;++i)
     {
         /*insert(i,min(i+k,T),1,-a[i]);
         if(i<k)        insert(i,i+1,inf,0);
         else        insert(i,i+1,U-L,0);*/
         if(i<=k)    insert(S0,i,inf,);
         insert(i,min(i+,T),U-L,);
                 insert(i,min(i+k,T),,-a[i]);
                 id[i]=t;
     }
     while(SP_spfa(S))Update();
     cout<<sum-ans<<endl;
     for(int i=;i<=n;++i) {
         if(e[id[i]^].c)    putchar('S');
         else                putchar('E');
     }
     //cout<<s<<endl;
     return ;
 }
    

代码