matlab中运用项目思维分析问题并解决问题

我们将沿着以下几步思考：
1.State the problem
关于这个例子陈述问题很简单.我们想写一个判定二元一次方程的程序：是否有两个实根，重复实根，或者两个复数根
2.Define the inputs and outputs
该程序要求输入二元一次方程的三个参数：a,b,c
输出方程根的判定情况
3.Design the algorithm
任务可被分为三个部分：input,processing,and output

Read the input data
Calculate the roots
Write out the roots

现在我们将以上三个部分划分为更小、更细的模块。
根据判别式的值，关于根的情况有三种，因此将执行这个算法用三分支的if结构是合理的

伪代码是：

允许用户定义三个变量 a,b,c
读取 a,b,and c
判别式discriminant <- b^2-4*a*c
if discriminant >0
x1 <- (-b+sqrt(discriminant ))/(2*a)
x2 <- (-b-sqrt(discriminant ))/(2*a)
写msg:二元一次方程有两个不相等实根！
显示两个实根
elseif discriminant == 0
x1 <- -b/(2*a)
写msg:二元一次方程有两个相等实根！
显示这个实根
else
real_part <- -b/(2*a)
image_part <- sqrt( abs(discriminant) )/(2*a)
写msg:二元一次方程有两个复数根
显示两个复数根
end
4.Turn the glgorithm into MATLAB statements
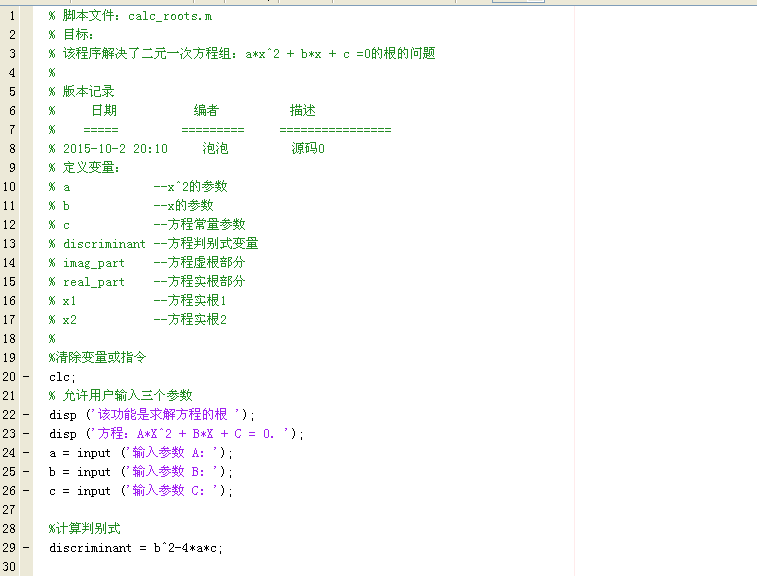
最终MATALAB如下所示：

%  脚本文件：calc_roots.m
%
% 目标：
% 该程序解决了二元一次方程组：a*x^ + b*x + c =0的根的问题
%
% 版本记录
%     日期           编者          描述
%    =====         =========     ================
% -- :     泡泡         源码
%
% 定义变量：
%
% a            --x^2的参数
% b            --x的参数
% c            --方程常量参数
% discriminant --方程判别式变量
% imag_part    --方程虚根部分
% real_part    --方程实根部分
% x1           --方程实根1
% x2           --方程实根2
%
%清除变量或指令
clc;
% 允许用户输入三个参数
disp ('该功能是求解方程的根 ');
disp ('方程：A*X^2 + B*X + C = 0. ');
a = input ('输入参数 A: ');
b = input ('输入参数 B: ');
c = input ('输入参数 C: ');

%计算判别式
discriminant = b^-*a*c;

%根据判别式分情况讨论
if discriminant >  %两个实根
     x1 = (-b+sqrt(discriminant ))/(*a)
     x2 = (-b-sqrt(discriminant ))/(*a)
     disp('二元一次方程有两个不相等实根！ ');
     fprintf (' x1=  %f\n' ,x1);
     fprintf (' x2=  %f\n' ,x2);
elseif discriminant ==
     x1 =  -b/(*a)
     disp('二元一次方程有两个相等实根！ ');
     fprintf (' x1=x2=  %f\n' ,x1);
else
     real_part = -b/(*a)
     image_part = sqrt( abs(discriminant) )/(*a)
     disp('二元一次方程有两个复数根 ');
     fprintf (' x1=  %f +i %f\n' ,real_part ,image_part );
     fprintf (' x2=  %f -i %f\n' ,real_part ,image_part );
end

5.Test the program
A B C 　　 根的情况
1 5 6 　　 -2，-3
1 4 4 　　 -2
1 2 5 　　 -1+/- i2
因此，该算法给出了三种情况的正确答案

附图：