遍历二叉树 - 基于队列的BFS

之前学过利用递归实现BFS二叉树搜索(http://www.cnblogs.com/webor2006/p/7262773.html),这次学习利用队列(Queue)来实现，关于什么时BFS这里不多说了，先贴张图来直观回忆下：

实现一个队列【采用数组实现】：

这时同样采用模版技术可以往队列中去放任何类型的数据，而这个队列同样是声明在头文件中，以便在需要用到队列的地方去随时包含它，下面先来定个初步框架：

/**
* 利用数组来实现队列
*/

template <typename T>

class queue
{
    T* data;//用数组来实现队列
    int head/* 头指向的位置 */, tail/* 尾指向的位置 */, size/* 当前队列存放的元素个数 */, data_length/* 总队列的大小 */;
public:
    queue(int length):head(), tail(), size(), data_length(length) {
        data = new T[length];
    }

    //入队列
    void push(T value) {

    }

    //出队列
    void pop() {

    }

    //取出队列最早的元素
    T top() {

    }

    //判断队列是否为空
    bool isEmpty() {

    }
};

具体实现如下：

/**
* 利用数组来实现队列
*/

template <typename T>

class queue
{
    T* data;//用数组来实现队列
    int head/* 头指向的位置 */, tail/* 尾指向的位置 */, size/* 当前队列存放的元素个数 */, data_length/* 总队列的大小 */;
public:
    queue(int length):head(), tail(), size(), data_length(length) {
        data = new T[length];
    }

    //入队列
    void push(T value) {
        if(size == data_length) {
            throw "queue is full";//如果队列已经满了则直接抛异常，实际可以去将数组扩容，这里简单处理，重在学习数据结构
        }
        data[head] = value;
        head = (head + ) % data_length;//这是为了循环利用，如果队列还有空间的话
        size++;
    }

    //出队列
    void pop() {
        if(isEmpty()) {
            throw "queue is empty";
        }
        tail = (tail + ) % data_length;//这是为了循环利用
        size--;
    }

    //取出队列最早的元素
    T top() {
        if(isEmpty())
            throw "You cannot get the top element from an empty queue";
        return data[tail];
    }

    //判断队列是否为空
    bool isEmpty() {
        return size == ;
    }
};

这里先来使用一下它，看入队跟出队的结果是否如预期：

编译运行:

对于上面的写法下面用图来将其整个过程画出来：

①、

创建一个大小为3的队列，其中head、tail指向数组0的位置，其中目前是一个size=0空数组

②、

往队列中插入元素1：

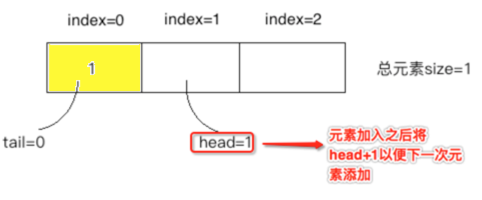
③、

往队列中插入元素2：

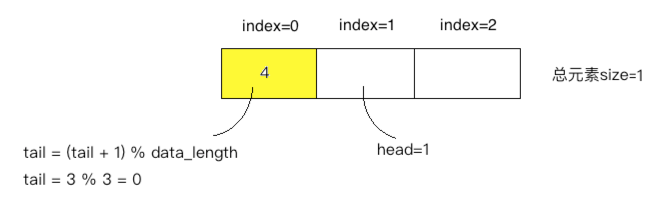
④、

往队列中插入元素3,这里需要注意啦！！！head会循环利用，指向数组0的位置：

⑤、

根据队列先进先出的原则拿最早放入的元素也就是tail所指向的元素：

⑥、

根据队列先进先出的原则拿最早放入的元素也就是tail所指向的元素：

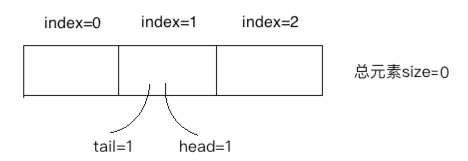
⑦、

根据队列先进先出的原则拿最早放入的元素也就是tail所指向的元素：

这时注意啦！！！tail跟head一样也会循环利用，又回到index=0的位置了：

⑧、

由于此时size=0了，所以会打印出"queue is empty"。

⑨、

⑩、

⑪、

由于此时size=0了，所以会打印出"queue is empty"。
总结：

1、添加元素放到head处，添加完成之后将head+1以便下次进行存放。

2、拿元素时是从tail处拿，拿完之后也是将tail+1以便拿下一个元素，因为是先进先出原则。

基于上节的实现来利用队列实现二叉树的BFS遍历：

先贴一下上节的代码，基于这个二叉树利用队列去实现：

#include <iostream>
#include "stack.h"
#include "queue.h"

//用来表示二叉树
struct treenode{
    int data;
    treenode* left;//左结点
    treenode* right;//右结点
    treenode(int value):data(value), left(nullptr), right(nullptr){}
};

//前序遍历
void pre_order(treenode* root){
    Stack<treenode*> stack;//声明一个栈
    treenode* current_node = root;
    while(current_node) {
        //1、首先打印当前结点，因为是前序遍历
        std::cout << current_node->data << std::endl;
        //2、如果存在右结点则将其入栈暂存,待左结点输出完之后再去处理这些右结点
        if(current_node->right) stack.push(current_node->right);
        //3、不断去处理左结点，直到左结点处理完了，则从栈中拿右点进行处理
        if(current_node->left)//如果有左结点，则将它做为当前处理的结点不断输出
            current_node = current_node->left;
        else {
            //这时左结点已经处理完了
            if(stack.isEmpty())//如果缓存栈已经为空了则说明整个二叉树的遍历结束了
                current_node = nullptr;
            else {
                //则取出栈顶的右结点进行处理，由于是后进先出，所以拿出来的永远是最新插入的右结点
                current_node = stack.top();
                stack.pop();//将其元素从栈顶弹出
            }

        }
    }
}

//利用队列实现BFS
void level_order(treenode* root){
    //TODO
}

int main(void) {

    //构建二叉树：
    //1、第一层根结点
    treenode* root = new treenode();
    //2、第二层结点
    root->left = new treenode();
    root->right = new treenode();
    //3、第三层结点
    root->left->left = new treenode();
    root->left->right = new treenode();
    root->right->left = new treenode();
    //4、第四层结点
    root->right->left->left = new treenode();

    pre_order(root);

    std::cout << "##################" << std::endl;

    level_order(root);

    return ;
}

其二叉树为：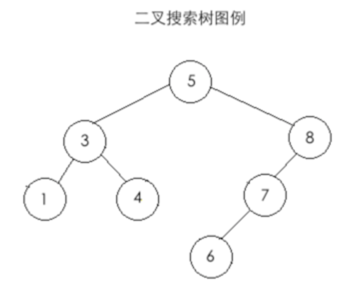

下面具体来实现level_order:

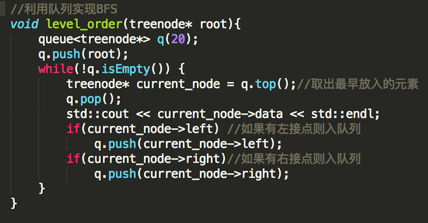
只要理解的队列的先进先出的特点上面的实现比较容易理解，不多解释，编译运行：

下面看一下它的时间复杂度：由于队列中有多少元素就会遍历多次次，所以很明显是O(n)。