【状压dp】Bzoj1294 围豆豆

题目

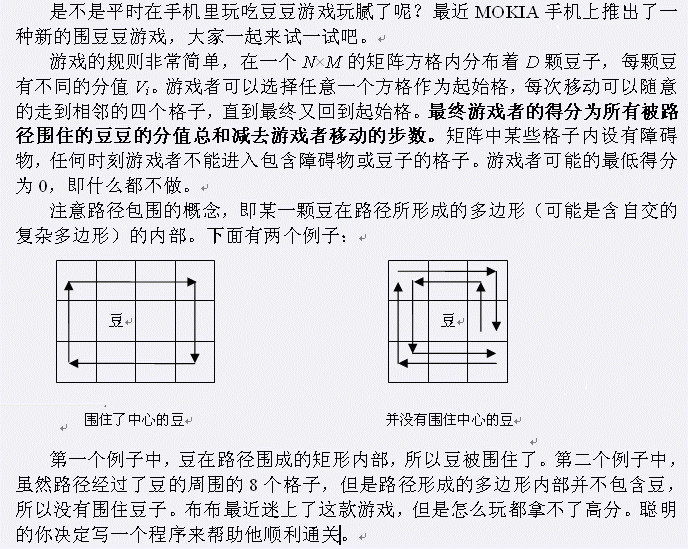
Input

第一行两个整数N和M，为矩阵的边长。 第二行一个整数D，为豆子的总个数。 第三行包含D个整数V1到VD，分别为每颗豆子的分值。 接着N行有一个N×M的字符矩阵来描述游戏矩阵状态，0表示空格，#表示障碍物。而数字1到9分别表示对应编号的豆子。

Output

仅包含一个整数，为最高可能获得的分值。

Sample Input

3 8
3
30 -100 30
00000000
010203#0
00000000

Sample Output

38

Hint

50%的数据满足1≤D≤3。 100%的数据满足1≤D≤9，1≤N, M≤10，-10000≤Vi≤10000。

分析

首先考虑一下点被包围的情况，在网上看到了一种不错的方法，也就是射线法。也就是从一个点向右做一条射线，如果与路线的交点个数为奇数，则这个点一定被围起来了。下边有几个图加强一下理解：

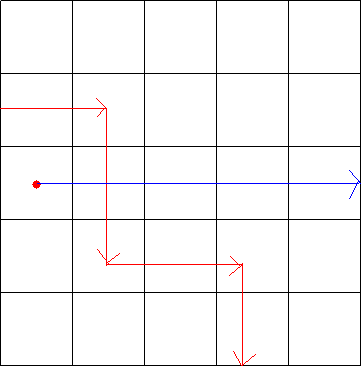
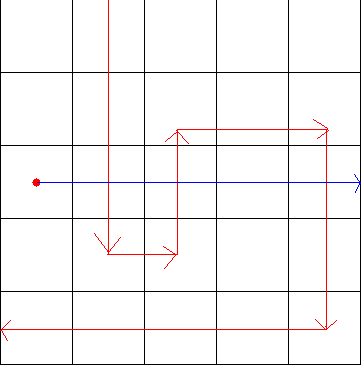
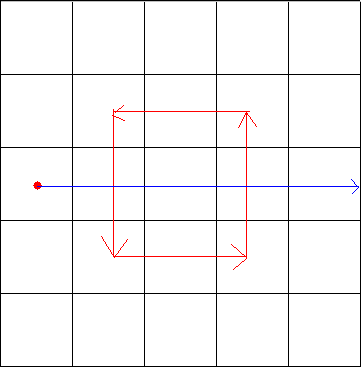
到这里我们可以看到如果交点奇数个，那么这个点就是被围起来的，反之则没有被围起来。

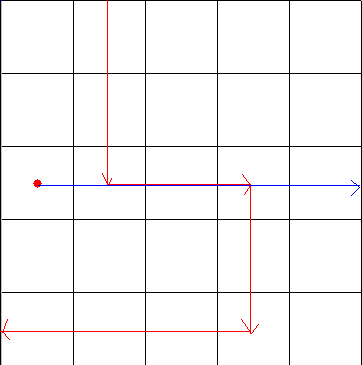
这个是一种特殊的情况，如果两条相交的边是同向的，那么也有可能包围这个点。于是乎我们就可以将射线向下移动半格。

因为这个转移是存在环的，所以选择spfa

代码

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <iostream>
 4 #include <queue>
 5 using namespace std;
 6 const int maxn=(1<<9)+3;
 7 int f[10][10][maxn],val[maxn];
 8 int inq[10][10][maxn],v[10],tr[10][10],dx[]={1,0,-1,0},dy[]={0,1,0,-1};
 9 char s[10][10];
10 queue<int> q1,q2,q3;
11 int n,m,K,ans;
12 int main()
13 {
14     scanf("%d%d%d",&n,&m,&K);
15     int i,j,k,S,T,a,b,c,d;
16     for(i=0;i<K;i++)scanf("%d",&v[i]);
17     for(i=1;i<(1<<K);i++){
18         for(j=0;j<K;j++)
19             if((i>>j)&1){
20                 val[i]=val[i^(1<<j)]+v[j];
21                 break;
22         }
23     }//射线法找围住的点
24     for(i=0;i<n;i++){
25         scanf("%s",s[i]);
26         S=0;
27         for(j=0;j<m;j++){
28             if(s[i][j]>='1'&&s[i][j]<='9')    S|=1<<(s[i][j]-'1');
29             tr[i][j]=S;
30         }
31     }//spfa
32     for(i=0;i<n;i++)
33         for(j=0;j<m;j++)
34             if(s[i][j]=='0'){
35                 memset(f,0x3f,sizeof(f));
36                 f[i][j][0]=0;
37                 q1.push(i),q2.push(j),q3.push(0);
38                 while(!q1.empty()){
39                     a=q1.front(),b=q2.front(),S=q3.front(),inq[a][b][S]=0,q1.pop(),q2.pop(),q3.pop();
40                     if(a==i&&b==j){
41                         ans=max(ans,val[S]-f[a][b][S]);//用f[a][b][S]表示当前走到(a,b)，已经围住的豆豆状态为S的最短路
42                     }
43                     for(k=0;k<4;k++){
44                         c=a+dx[k],d=b+dy[k];
45                         if(c<0||c==n||d<0||d==m||s[c][d]!='0')    continue;
46                         T=S;
47                         if(k==0)T^=tr[a][b];
48                         if(k==2)T^=tr[c][d];
49                         if(f[c][d][T]>f[a][b][S]+1){
50                             f[c][d][T]=f[a][b][S]+1;
51                             if(!inq[c][d][T])    inq[c][d][T]=1,q1.push(c),q2.push(d),q3.push(T);
52                         }
53                     }
54                 }
55             }
56     printf("%d",ans);
57     return 0;
58 }

（PS：这道题本人还不是理解的特别透彻，只是大致理解了思路和做法，代码的内容还要细细钻研琢磨。）