鱼塘钓鱼（fishing）（信息学奥赛一本通 1373）

【问题描述】

有N个鱼塘排成一排（N<100），每个鱼塘中有一定数量的鱼，例如：N=5时，如下表：

即：在第1个鱼塘中钓鱼第1分钟内可钓到10条鱼，第2分钟内只能钓到8条鱼，……，第5分钟以后再也钓不到鱼了。从第1个鱼塘到第2个鱼塘需要3分钟，从第2个鱼塘到第3个鱼塘需要5分钟，……

【编程任务】 　　

给出一个截止时间T(T<1000)，设计一个钓鱼方案，从第1个鱼塘出发，希望能钓到最多的鱼。 　　假设能钓到鱼的数量仅和已钓鱼的次数有关，且每次钓鱼的时间都是整数分钟。

【输入格式】 　　

输入文件共5行，分别表示： 　　

第1行为N； 　　

第2行为第1分钟各个鱼塘能钓到的鱼的数量，每个数据之间用一空格隔开； 　　

第3行为每过1分钟各个鱼塘钓鱼数的减少量，每个数据之间用一空格隔开； 　　

第4行为当前鱼塘到下一个相邻鱼塘需要的时间； 　　

第5行为截止时间T；

【输出格式】 　　

输出文件仅一个整数（不超过231-1），表示你的方案能钓到的最多的鱼。

【输入样例】

5 10 14 20 16 9 2 4 6 5 3 3 5 4 4 14

【输出样例】 　　　

76

---

【解法一】暴力

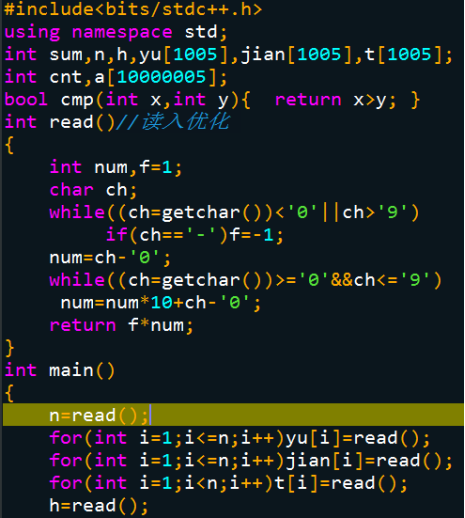
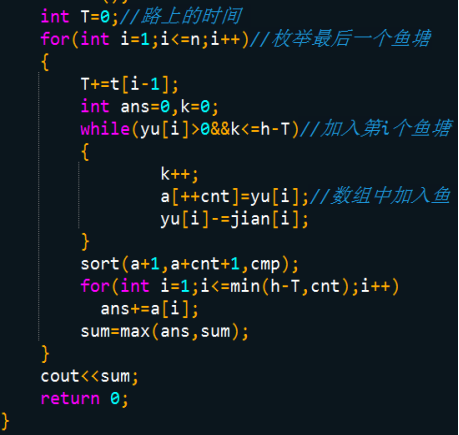
（读入优化后居然真的可以过！！！好水的数据啊）

【解法二】

建立以fish为关键字的大根堆，包括能钓到鱼的数量和池塘的编号。然后借助枚举创造条件，实现复杂度为O（m*nlogn）的算法。

#include <iostream>
#include <cstdio>
using namespace std;
struct Data
{
  int fish, lake;                               //堆中结点的信息
};
Data heap[];
int t[], f[], d[];
int Max, k, t1;
void maintain(int i)                            //维护堆
{
  Data a;
  int next;
  a = heap[i];
  next = i * ;
while(next <= k)
  {
    if(next < k && heap[next].fish < heap[next + ].fish)
    next++;
    if(a.fish < heap[next].fish)
    {
      heap[i] = heap[next];
      i = next;
      next *= ;
    }
    else break;
  }
  heap[i] = a;
}
void work()
{
  int i, j, m, n;
  cin >> n;
  for(i =  ; i <= n ; i++) cin >> f[i];
  for(i =  ; i <= n ; i++) cin >> d[i];
  for(i =  ; i < n ; i++) cin >> t[i];
  cin >> m;
  for(k =  ; k <= n ; k++) //枚举最远走到的池塘的编号
  {
    int Time = m - t1; //计算剩余时间
    int ans = ;
    for(i =  ; i <= k ; i++) //收集能够钓鱼的池塘的资料
    {
      heap[i].fish = f[i];
      heap[i].lake = i;
    }
    for(i =  ; i <= k /  ; i++) maintain(i);  //堆的初始化
    while(Time >  && heap[].fish > )
    {
      ans += heap[].fish;                     //贪心选取鱼最多的池塘
      heap[].fish -= d[heap[].lake];            //修改鱼的数量
      maintain();                           //堆维护
      Time--;                               //剩余时间变少
    }
if(ans > Max) Max = ans;                   //刷新最优解
    t1 += t[k];                               //累计走路需要的时间
  }
  cout << Max << endl;
}

int main()
{
  work();
  return ;
}

使用STL的版本：

#include <iostream>
#include <cstdio>
#include <queue>
#define fish first
#define lake second
using namespace std;
priority_queue <pair<int, int> > heap;
int t[], f[], d[];
int ans, m, Max, n, k, t1, Time;
void work()
{
    int i, j;
    cin >> n;
    for(i =  ; i <= n ; i++) cin >> f[i];
    for(i =  ; i <= n ; i++) cin >> d[i];
    for(i =  ; i < n ; i++) cin >> t[i];
    cin >> m;
    for(k =  ; k <= n ; k++) //枚举最远走到的池塘的编号
    {
        Time = m - t1;            //计算剩余时间
        ans = ;
        for(i =  ; i <= k ; i++)   //收集能够钓鱼的池塘的资料
        heap.push(make_pair(f[i], i));

         while(Time >  && heap.top().fish > )
        {
            pair<int, int> a = heap.top();
            heap.pop();
            ans += a.fish; //贪心选取鱼最多的池塘
            a.fish -= d[a.lake]; //修改鱼的数量
            heap.push(a);                     //堆维护
            Time--;                       //剩余时间变少
        }
    if(ans > Max) Max = ans; //刷新最优解
       t1 += t[k]; //累计走路需要的时间
    }
    cout << Max << endl;
}

int main()
{
    work();
    return ;
}