SVM原理 （转载）

1. 线性分类SVM面临的问题

　　　　有时候本来数据的确是可分的，也就是说可以用 线性分类SVM的学习方法来求解，但是却因为混入了异常点，导致不能线性可分，比如下图，本来数据是可以按下面的实线来做超平面分离的，可以由于一个橙色和一个蓝色的异常点导致我们没法直接线性分类。

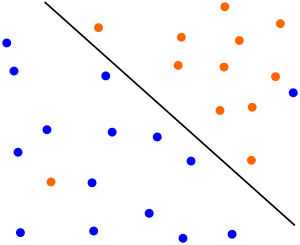
　　　　另外一种情况没有这么糟糕到不可分，但是会严重影响我们模型的泛化预测效果，比如下图，本来如果我们不考虑异常点，SVM的超平面应该是下图中的红色线所示，但是由于有一个蓝色的异常点，导致我们学习到的超平面是下图中的粗虚线所示，这样会严重影响我们的分类模型预测效果。

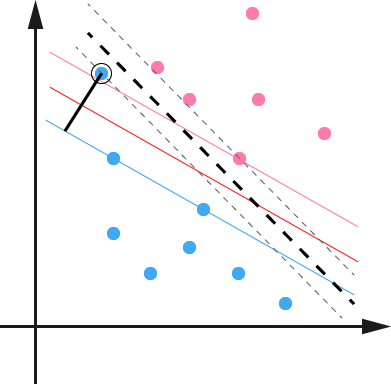
　　　　如何解决这些问题呢？SVM引入了软间隔最大化的方法来解决。

2. 线性分类SVM的软间隔最大化

　　　　所谓的软间隔，是相对于硬间隔说的，我们可以认为上一篇线性分类SVM的学习方法属于硬间隔最大化。

　　　　回顾下硬间隔最大化的条件：

　　　　　　　　　　　　

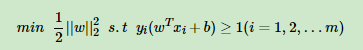
　　　　接着我们再看如何可以软间隔最大化呢？

　　　　SVM对训练集里面的每个样本(xi,yi)(xi,yi)引入了一个松弛变量ξi≥0ξi≥0,使函数间隔加上松弛变量大于等于1，也就是说：　　

　　　　　　　　　　　　　　　　　　　　　　　　

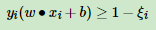
　　　　对比硬间隔最大化，可以看到我们对样本到超平面的函数距离的要求放松了，之前是一定要大于等于1，现在只需要加上一个大于等于0的松弛变量能大于等于1就可以了。当然，松弛变量不能白加，这是有成本的，每一个松弛变量ξiξi, 对应了一个代价ξiξi，这个就得到了我们的软间隔最大化的SVM学习条件如下：

　　　　　　　　　　　　　　　　　　　　

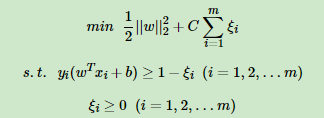
　　　　这里,C>0C>0为惩罚参数，可以理解为我们一般回归和分类问题正则化时候的参数。CC越大，对误分类的惩罚越大，CC越小，对误分类的惩罚越小。

　　　　也就是说，我们希望12||w||2212||w||22尽量小，误分类的点尽可能的少。C是协调两者关系的正则化惩罚系数。在实际应用中，需要调参来选择。

　　　　这个目标函数的优化和上一篇的线性可分SVM的优化方式类似，我们下面就来看看怎么对线性分类SVM的软间隔最大化来进行学习优化。

3. 线性分类SVM的软间隔最大化目标函数的优化

　　　　和线性可分SVM的优化方式类似，我们首先将软间隔最大化的约束问题用拉格朗日函数转化为无约束问题如下：

　　　　　　　　　　

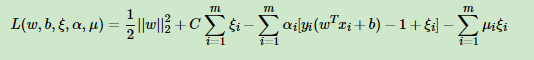
　　　　其中 μi≥0,αi≥0μi≥0,αi≥0,均为拉格朗日系数。

　　　　也就是说，我们现在要优化的目标函数是：

　　　　　　　　　　　　

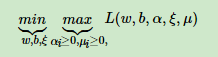
　　　　这个优化目标也满足KKT条件，也就是说，我们可以通过拉格朗日对偶将我们的优化问题转化为等价的对偶问题来求解如下：

　　　　　　　　　　　　

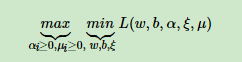
　　　　我们可以先求优化函数对于w,b,ξw,b,ξ的极小值, 接着再求拉格朗日乘子αα和 μμ的极大值。

　　　　首先我们来求优化函数对于w,b,ξw,b,ξ的极小值，这个可以通过求偏导数求得：

　　　　　　　　　　　　

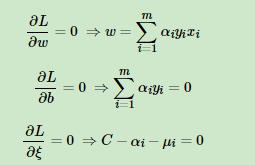
　　　　好了，我们可以利用上面的三个式子去消除ww和bb了。

　　　　　　

　　　　　　

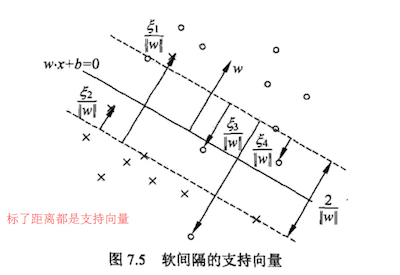
4. 软间隔最大化时的支持向量

　　　　在硬间隔最大化时，支持向量比较简单，就是满足yi(wTxi+b)−1=0yi(wTxi+b)−1=0就可以了。根据KKT条件中的对偶互补条件α∗i(yi(wTxi+b)−1)=0αi∗(yi(wTxi+b)−1)=0，如果α∗i>0αi∗>0则有yi(wTxi+b)=1yi(wTxi+b)=1 即点在支持向量上，否则如果α∗i=0αi∗=0则有yi(wTxi+b)≥1yi(wTxi+b)≥1，即样本在支持向量上或者已经被正确分类。

　　　　

　　　　　　　　　　　　　　

5. 软间隔最大化的线性可分SVM的算法过程