Tree 树形结构

一、树的基本概念

（1）树（Tree）的概念：树是一种递归定义的数据结构，是一种重要的非线性数据结构。

树可以是一棵空树，它没有任何的结点；也可以是一棵非空树，至少含有一个结点。

（2）根（Root）：有且仅有一个结点的非空树，那个结点就是根。

（3）子树（Subtree）：在一棵非空树中，除根外，其余所有结点可以分为m（m≥0）个互不相交的集合。每个集合本身又是一棵树，称为根的子树。

（4）结点（Node）：表示树中的元素及若干指向其子树的分支。

（5）结点的度（Degree）：一个结点拥有的子树数目称为该结点的度。

（6）叶子结点（Leaf）：度为0的结点。

（7）孩子（Child）：结点子树的根称为该结点的孩子。

（8）双亲（Parents）：孩子结点的上层结点叫该结点的双亲。

（9）兄弟（Sibling）：同一双亲的孩子。

（10）树的度：一棵树中最大的结点度数。

（11）结点的层次（Level）：从根结点开始定义根为第一层，它的孩子为第二层，依此类推。

（12）深度（Depth）：树中结点最大层次的值。

（13）有序树：树中的各子树自左向右有序的称为有序树。

（14）无序树：树中的各子树自左向右无序的称为无序树。

（15）森林（Forest）：是m（m≥0）棵互不相交的树的集合。

（16）祖先：是指从根结点到该结点之间所有的结点。

如图所示：

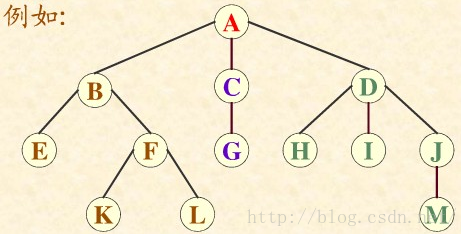
A是根结点，A结点的度是3，D结点的度是3；因为3是结点的度的最大值，所以这棵树的度是3；E、G、H、I、K、L和M是叶子结点。

A在树的第一层，B、C、D在树的第二层，E、F、G、H、I、J在树的第三层，K、L、M在树的第四层；树的深度是4。

树从左往右是有序的，这是一棵有序树；E结点的祖先是A、B。
 

二 二叉树

　　概念：二叉树又叫二分树，它的特点是每个结点最多只有二棵子树，也就是二叉树中没有度大于2的结点。二叉树的子树有左右之分，严格区分左孩子、右孩子，其次序不能颠倒。

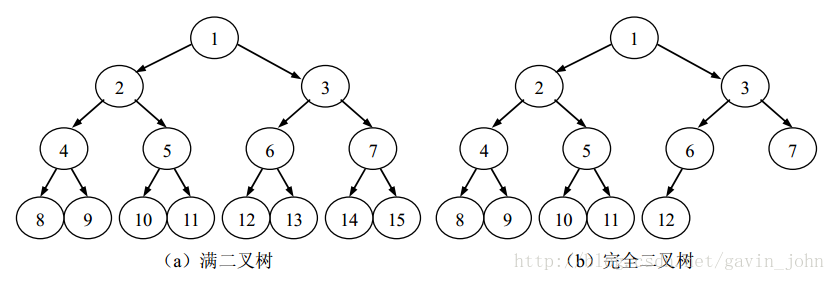
满二叉树

　　 概念：一棵深度为k且有2^k-1个结点的二叉树称为满二叉树。

完全二叉树

　　概念：可以对满二叉树的结点进行连续编号，约定编号从根结点起，自上而下，自左至右。由此可以引出完全二叉树的定义。深度为k的，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应，称之为完全二叉树。

　　完全二叉树的特点是：

　　（1）叶子结点只可能在层次最大的两层上出现；（2）对任一结点，若其右分支下的子孙的最大层次为l，则其左分支下的子孙的最大层次必为l或l+1。

三 性质

　　性质1： 在二叉树的第i层上至多有2i-1个结点（i>=1）

　　性质2： 深度为k的二叉树至多有2k-1个结点，（k>=1）.

　　性质3： 对任何一棵二叉树T，如果其终端结点数位n0，度为2的结点数为n2，则 n0 = n2 + 1

　　性质4： 具有n个结点的完全二叉树的深度为 ⌊log2n⌋+1　　

　　性质5： 如果对一棵有n个结点的完全二叉树（其深度为 ⌊log2n⌋+1 ）的结点按层序编号（从第1层到第 ⌊log2n⌋+1 层，每层从左到右），则对任一结点i(1<=i<=n)，有：

　　　　（1）如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲PARENT(i)是结点⌊i/2⌋。

　　　　（2）如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子LCHILD(i)是结点2i。

　　　　（3）如果2i+1>n，则结点i无右孩子；否则其右孩子RCHILD(i)是结点2i+1。

四 python 代码

代码

class Node:
    "定义节点类"
    def __init__(self,item):
        self.item=item
        self.lchild=None
        self.rchild=None

class Tree:
    "定义树类"
    def __init__(self):
        self.root=None

    def add(self,item):
        node=Node(item)
        if not self.root:
            self.root=node
            return
        queue=[self.root,]
        while queue:
            current_node=queue.pop(0)
            if current_node.lchild is None:
                current_node.lchild=node
                return
            else:
                queue.append(current_node.lchild)
            if current_node.rchild is None:
                current_node.rchild=node
                return
            else:
                queue.append(current_node.rchild)
    def breadth_travel(self):
        '''广度遍历'''
        if self.root is None:
            return
        queue=[self.root,]

        while queue:
            current_node=queue.pop(0)
            print(current_node.item,end=" ")
            if current_node.lchild is not None:
                queue.append(current_node.lchild)
            if current_node.rchild is not None:
                queue.append(current_node.rchild)

    def preorder(self,node):
        '''先序遍历----根->左->右'''
        if node is None:
            return
        print(node.item,end=" ")
        self.preorder(node.lchild)
        self.preorder(node.rchild)

    def inorder(self,node):
        '''中序遍历----左->中->右'''
        if node is None:
            return
        self.inorder(node.lchild)
        print(node.item,end=" ")
        self.inorder(node.rchild)

    def postorder(self,node):
        '''后序遍历----左->右->中'''
        if node is None:
            return
        self.postorder(node.lchild)
        self.postorder(node.rchild)
        print(node.item,end=" ")

if __name__ == '__main__':
    tree=Tree()
    tree.add(0)
    tree.add(1)
    tree.add(2)
    tree.add(3)
    tree.add(4)
    tree.add(5)
    tree.add(6)
    tree.add(7)
    tree.add(8)
    tree.add(9)
    print('-----广度遍历-----')
    tree.breadth_travel()
    print('\n-----深度先序遍历-----')
    tree.preorder(tree.root)
    print('\n-----深度中序遍历-----')
    tree.inorder(tree.root)
    print('\n-----深度后序遍历-----')
    tree.postorder(tree.root)

树形结构

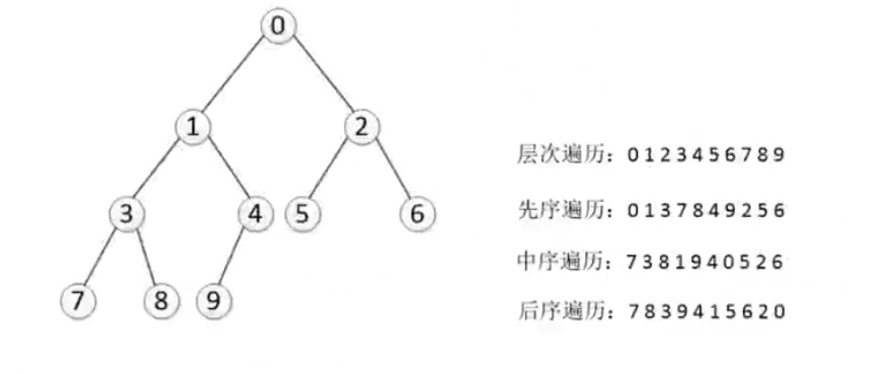
结果

-----广度遍历-----
0 1 2 3 4 5 6 7 8 9
-----深度先序遍历-----
0 1 3 7 8 4 9 2 5 6
-----深度中序遍历-----
7 3 8 1 9 4 0 5 2 6
-----深度后序遍历-----
7 8 3 9 4 1 5 6 2 0 

好文推荐

原文：https://blog.csdn.net/tfygg/article/details/46763389

原文：https://blog.csdn.net/gavin_john/article/details/72312276