Algorithm(4th) 1.5 union-find算法

问题描述

问题输入是一对整数对，每个整数都代表一个对象，一对整数”p,q“表示 ”p与q相连“（具有自反性，传递性，对称性，被归到一个等价类里），要求编写程序来筛除在输入时就已经在一个等价类里的整数对。这个算法可以在计算机网络连结方面发挥作用：每个整数相当于计算机，整数对相当于网络间的连结，我们的程序可以判断为了使p，q两个计算机连结，需不需要添加一个新的线路。

具体思想

1.根节点判断

我们可以通过一个“概念上”的森林来实现我们的程序。我们把union-find算法打包成一个类，在其中设置一个名为id的数组用来存放每个节点的下一个连结对象，这样可以通过接受一个数组的秩来不断访问它所连结的下一个对象，直至到一个秩和所存储对象节点号相同的节点（根节点）。而比较两个节点的根节点就可以判断他们是否连在同一个根节点上，进而判断出两个节点是否已经连结。

2.加权连结

如果判断两个节点没有连结到一个根节点，我们就对他们的根节点进行连结。这时就会产生一个问题：p去连q还是q去连p。这里我们采用加权的算法：引入一个数组sz（size）来记录每个节点作为根节点时树中的节点数，把它作为节点的权值。每次进行根节点连结时，我们总是把权值小的根节点连结到权值大的根节点上。这样的好处是可以极大地降低树的高度的增加速度（最大程度降速的方式是把树高度作为权值的加权连结，但经过路径压缩后，这种方式变得没有必要），从而降低查找根节点时的时间量级。在最坏的情况下，要连结的树的大小总是相等的，且都是2的幂，则把所有的N个节点合成一个树，这个树的高度是底数为2的N的对数。

致使查找要检索的高度也达到O(logN)。



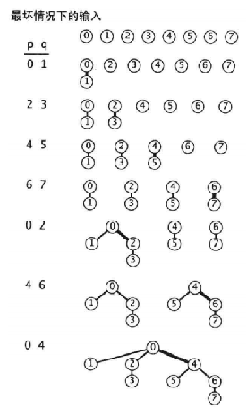
PS:本图取自Algorithm(4th)中译版P146（原版P229）

实现代码

#include<iostream>
#include<vector>
#include<random>

using namespace std;

//WeightedQuickUnion(加权快速连结)
class WQU {
	vector<int> id;
	vector<int> sz;
	int count = 0;
	int numberOfSite = 0;
public:
	int find(int p);
	void Union(int p, int q);
	int get_count() { return count; }
	bool connected(int p, int q);
	int Count(int n);
	int newSite();
};

bool WQU::connected(int p, int q) {
	if (p >= numberOfSite || q >= numberOfSite) {
		throw runtime_error("Site does not exist");
	}
	return find(p) == find(q);
}

//压缩路径find，递归，只修改查找时经历节点的连结
int WQU::find(int p) {
	if (p >= numberOfSite) {
		throw runtime_error("Site does not exist");
	}
	if (p == id[p]) { return p; }
	return id[p] = find(id[p]);
}

void WQU::Union(int p, int q) {
	if (p >= numberOfSite || q >= numberOfSite) {
		throw runtime_error("Site does not exist");
	}
	int rp = find(p);
	int rq = find(q);
	if (rp == rq) { return; }
	if (sz[rp] < sz[rq]) {
		id[rp] = rq;
		sz[rq] += sz[rp];
	}
	else {
		id[rq] = rp;
		sz[rp] += sz[rq];
	}
	--count;
}

//测试随机生成数据最终连在一棵树上所需的连结条数
int WQU::Count(int n) {
	while (n > numberOfSite) { newSite(); }
	while (get_count() != 1) {
		int p = rand() % n;
		int q = rand() % n;
		cout << p << ' ' << q << endl;
		if (!connected(p, q)) {
			Union(p, q);
		}
	}
	int cnt = 0;
	for (size_t i = 0; i < id.size(); ++i) {
		if (i != id[i]) {
			++cnt;
		}
	}
	return cnt;
}

//创建一个参与连结的新节点，返回它的值
int WQU::newSite() {
	id.push_back(numberOfSite);
	sz.push_back(1);
	++count;
	return numberOfSite++;
}

int main() {
	int n;
	cin >> n;
	WQU temp;
	cout << temp.Count(n);
	return 0;
}

find采用递归压缩路径。在不改变根节点的情况下，令被查找过的节点指向其根节点，从而降低被查找过的节点的深度，进而降低再次查找时的时间复杂度。