c#数字图像处理（五）全等级直方图灰度拉伸

灰度拉伸也属于线性点运算的一种,也可以通过上一节的程序得到。但由于它在点运算的特殊性,所以把它单独列出来进行介绍。

灰度拉伸定义

如果一幅图像的灰度值分布在全等级灰度范围内,即在0~255之间,那么它更容易被区别确认出来。

灰度拉伸,也称对比度拉伸,是一种简单的线性点运算。它扩展图像的直方图,使其充满整个灰度等级范围内。

设f(x,y)为输入图像,它的最小灰度级A和最大灰度级B的定义为:

A=min[f(x,y) B=max[f(x,y)]

我们的目标是按照公式   g(x, y)=pf(x,y)+L   ,  把A和B分别线性映射到0和255,因此,最终的图像g(x,y)为:

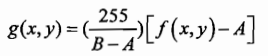
private void stretch_Click(object sender, EventArgs e)
        {
            Stretch(curBitmpap, out curBitmpap);
            Invalidate();
        }

        /// <summary>
        /// 全等级灰度拉伸 （图像增强）
        /// </summary>
        /// <param name="srcBmp">原图像</param>
        /// <param name="dstBmp">处理后图像</param>
        /// <returns>处理成功 true 失败 false</returns>
        public static bool Stretch(Bitmap srcBmp, out Bitmap dstBmp)
        {
            if (srcBmp == null)
            {
                dstBmp = null;
                return false;
            }
            double pR = 0.0;//斜率
            double pG = 0.0;//斜率
            double pB = 0.0;//斜率
            byte minGrayDegree = ;
            byte maxGrayDegree = ;
            byte minGrayDegreeR = ;
            byte maxGrayDegreeR = ;
            byte minGrayDegreeG = ;
            byte maxGrayDegreeG = ;
            byte minGrayDegreeB = ;
            byte maxGrayDegreeB = ;
            dstBmp = new Bitmap(srcBmp);
            Rectangle rt = new Rectangle(, , dstBmp.Width, dstBmp.Height);
            BitmapData bmpData = dstBmp.LockBits(rt, ImageLockMode.ReadWrite, PixelFormat.Format24bppRgb);

            unsafe
            {
                for (int i = ; i < bmpData.Height; i++)
                {
                    byte* ptr = (byte*)bmpData.Scan0 + i * bmpData.Stride;
                    for (int j = ; j < bmpData.Width; j++)
                    {
                        if (minGrayDegreeR > *(ptr + j *  + ))
                            minGrayDegreeR = *(ptr + j *  + );
                        if (maxGrayDegreeR < *(ptr + j *  + ))
                            maxGrayDegreeR = *(ptr + j *  + );
                        if (minGrayDegreeG > *(ptr + j *  + ))
                            minGrayDegreeG = *(ptr + j *  + );
                        if (maxGrayDegreeG < *(ptr + j *  + ))
                            maxGrayDegreeG = *(ptr + j *  + );
                        if (minGrayDegreeB > *(ptr + j * ))
                            minGrayDegreeB = *(ptr + j * );
                        if (maxGrayDegreeB < *(ptr + j * ))
                            maxGrayDegreeB = *(ptr + j * );
                    }
                }
                pR = 255.0 / (maxGrayDegreeR - minGrayDegreeR);
                pG = 255.0 / (maxGrayDegreeG - minGrayDegreeG);
                pB = 255.0 / (maxGrayDegreeB - minGrayDegreeB);
                for (int i = ; i < bmpData.Height; i++)
                {
                    byte* ptr1 = (byte*)bmpData.Scan0 + i * bmpData.Stride;
                    for (int j = ; j < bmpData.Width; j++)
                    {
                        *(ptr1 + j * ) = (byte)((*(ptr1 + j * ) - minGrayDegreeB) * pB + 0.5);
                        *(ptr1 + j *  + ) = (byte)((*(ptr1 + j *  + ) - minGrayDegreeG) * pG + 0.5);
                        *(ptr1 + j *  + ) = (byte)((*(ptr1 + j *  + ) - minGrayDegreeR) * pR + 0.5);
                    }
                }
            }
            dstBmp.UnlockBits(bmpData);
            return true;
        }

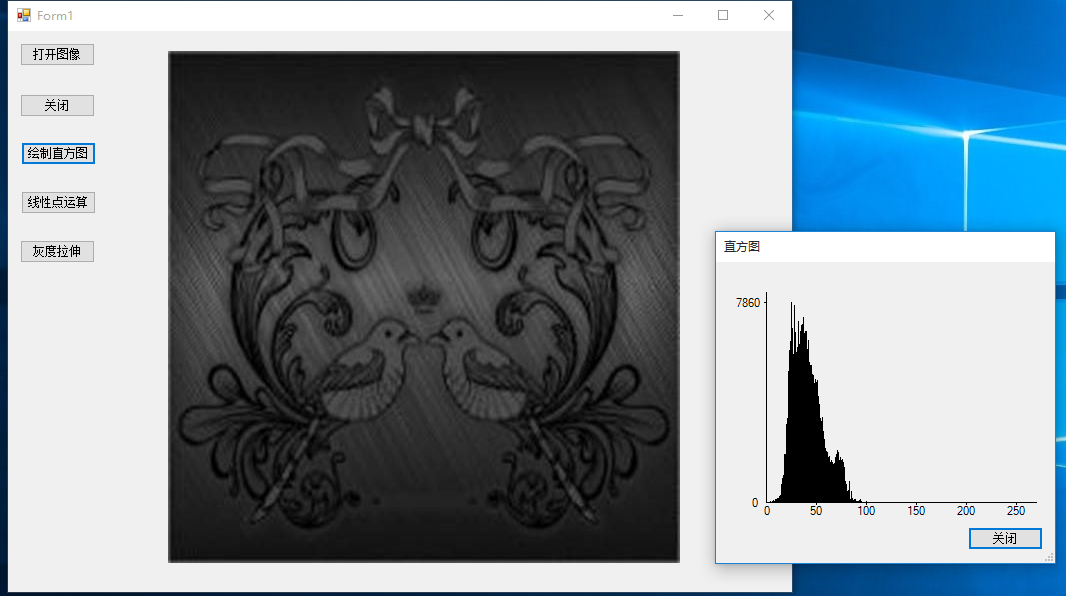
增强后：