[bzoj1297] [洛谷P4159] [SCOI2009] 迷路

Description###

windy在有向图中迷路了。 该有向图有 N 个节点，windy从节点 0 出发，他必须恰好在 T 时刻到达节点 N-1。 现在给出该有向图，你能告诉windy总共有多少种不同的路径吗？ 注意：windy不能在某个节点逗留，且通过某有向边的时间严格为给定的时间。

Input###

第一行包含两个整数，N T。 接下来有 N 行，每行一个长度为 N 的字符串。 第i行第j列为'0'表示从节点i到节点j没有边。 为'1'到'9'表示从节点i到节点j需要耗费的时间。

Output###

包含一个整数，可能的路径数，这个数可能很大，只需输出这个数除以2009的余数。

Sample Input###

【输入样例一】

2 2

11

00

【输入样例二】

5 30

12045

07105

47805

12024

12345

Sample Output###

【输出样例一】

1

【样例解释一】

0->0->1

【输出样例二】

852

HINT###

30%的数据，满足 2 <= N <= 5 ； 1 <= T <= 30 。 100%的数据，满足 2 <= N <= 10 ； 1 <= T <= 1000000000 。

---

想法##

dp方程还是很显然的，设 \(f[i][j]\) 表示在第i时刻到达点j的方案数

$f[i][j]=\sum\limits_{e[k][i]\neq 0} f[j-e[k][i]][k] $ （\(e[i][j]\)为结点i到结点j花费的时间）

然而T这么大肯定是过不了的。

这时注意到n很小，像这种变量一大一小的果断矩阵乘法。

由于\(e[i][j] \leq 9\) ， 所以计算某一时间时只会用到前9个时间。

不同于“计算斐波那契数列”那种基本的矩阵乘法，这里的f不是一维的，而是二维的。

但没关系，由于会用到的f值比较少，所以可以把二维强行拉成一维。

像这样：

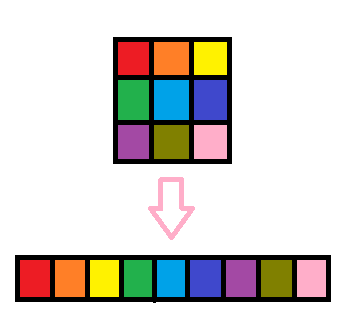
然后就像普通的矩阵乘法一样搞就好了。

---

代码##

细节有点多，要想清楚一些。

P.S. 代码中的转移并不是上面所说的那种，而是用\(f[i][j]\)更新\(f[i+e[j][k]][k]\)，这样写起来更方便。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

#define P 2009

using namespace std;

const int SZ = 100;

struct matrix{
	int a[SZ][SZ];
	matrix() { memset(a,0,sizeof(a)); }
	void init() { for(int i=0;i<SZ;i++) a[i][i]=1; }
	matrix operator * (matrix &b) const{
	    matrix c;
	    for(int i=0;i<SZ;i++)
	    	for(int j=0;j<SZ;j++)
				for(int k=0;k<SZ;k++)
					(c.a[i][j]+=a[i][k]*b.a[k][j])%=P;
		return c;
	}
	matrix operator *= (matrix &b) { return *this=*this*b; }
};

matrix Pow_mod(matrix x,int y){
	matrix ret; ret.init();
	while(y){
		if(y&1) ret*=x;
		x*=x;
		y>>=1;
	}
	return ret;
}

int n,T;
char e[15][15];

int main()
{
	scanf("%d%d",&n,&T);
	for(int i=1;i<=n;i++)
	    scanf("%s",e[i]+1);

	matrix a,b;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(e[i][j]!='0') {
				a.a[(i-1)*9][(j-1)*9+e[i][j]-'0'-1]++;
			}
	for(int i=1;i<=n;i++)
		for(int j=0;j<8;j++) a.a[(i-1)*9+j+1][(i-1)*9+j]++;
	b.a[0][0]=1;
	a=Pow_mod(a,T);
	b*=a;
	printf("%d\n",b.a[0][(n-1)*9]);

	return 0;
}