matlib实现梯度下降法(序一）

数据来源：http://archive.ics.uci.edu/ml/datasets/Combined+Cycle+Power+Plant

数据描述：

有四个输入特征，这些数据来自电厂，这四个特征和电量输入有关系，现在通过线性回归求它们之间关系的模型参数。
- 温度，Temperature (T) in the range 1.81°C and 37.11°C,
- 大气压，Ambient Pressure (AP) in the range 992.89-1033.30 milibar,
- 相对湿度，Relative Humidity (RH) in the range 25.56% to 100.16%
- 排气容积，Exhaust Vacuum (V) in teh range 25.36-81.56 cm Hg
- 输出电力百万瓦：Net hourly electrical energy output (EP) 420.26-495.76 MW
The averages are taken from various sensors located around the plant that record the ambient variables every second. The variables are given without normalization.

注意，这些数据没有归一化，由于四个特征大小差别很大，所以要进行归一化操作，具体操作参照http://www.cnblogs.com/mikewolf2002/p/7560748.html 3.4节。

总共数据9568条数据，我们选取前9000条数据为训练数据，放在train.txt，后面568条数据为验证数据,放在verify.txt

clear all; close all; clc;
data = load('train.txt');
x = data(:,1:4); %温度，大气压，湿度，排气容积
y = data(:,5); %输出电力
m = length(y); % 样本数目
x = [ones(m, 1), x]; % 输入特征增加一列，x0=1
meanx = mean(x);%求均值
sigmax = std(x);%求标准偏差
x(:,2) = (x(:,2)-meanx(2))./sigmax(2);
x(:,3) = (x(:,3)-meanx(3))./sigmax(3);
x(:,4) = (x(:,4)-meanx(4))./sigmax(4);
x(:,5) = (x(:,5)-meanx(5))./sigmax(5);
theta = zeros(size(x(1,:)))'; % 初始化theta

MAX_ITR = 1500;%最大迭代数目
alpha = 0.1; %学习率
i = 0;
while(i<MAX_ITR)
   grad =  (1/m).*x' * ((x * theta) - y);%求出梯度
   theta = theta - alpha .* grad;%更新theta
   if(i>2)
       delta = old_theta-theta;
       delta_v = delta.*delta;
       if(delta_v<0.000000000000001)%如果两次theta的内积变化很小，退出迭代
           break;
       end
   end
   old_theta = theta;
   %theta
   i=i+1;
end
data1 = load('verify.txt');
x1 = data1(:,1:4); %温度，压力，适度，压强
y1 = data1(:,5); %输出电力
m1 = length(y1); % 样本数目
x1 = [ones(m1, 1), x1]; % 输入特征增加一列，x0=1

meanx1 = mean(x1);%求均值
sigmax1 = std(x1);%求标准偏差
x1(:,2) = (x1(:,2)-meanx1(2))./sigmax1(2);
x1(:,3) = (x1(:,3)-meanx1(3))./sigmax1(3);
x1(:,4) = (x1(:,4)-meanx1(4))./sigmax1(4);
x1(:,5) = (x1(:,5)-meanx1(5))./sigmax1(5);

y2 = x1*theta;
y2

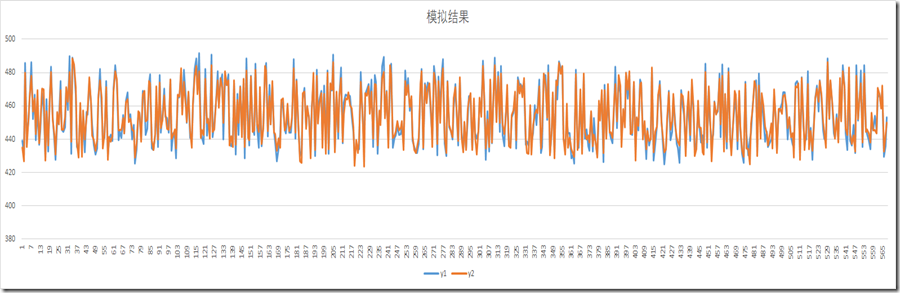
y1为原始验证数据结果，y2为预测结果，从下面图中看到y1/y2都挺接近的。