软件安装：树上分组DP/tarjan缩点/（也许基环树？）

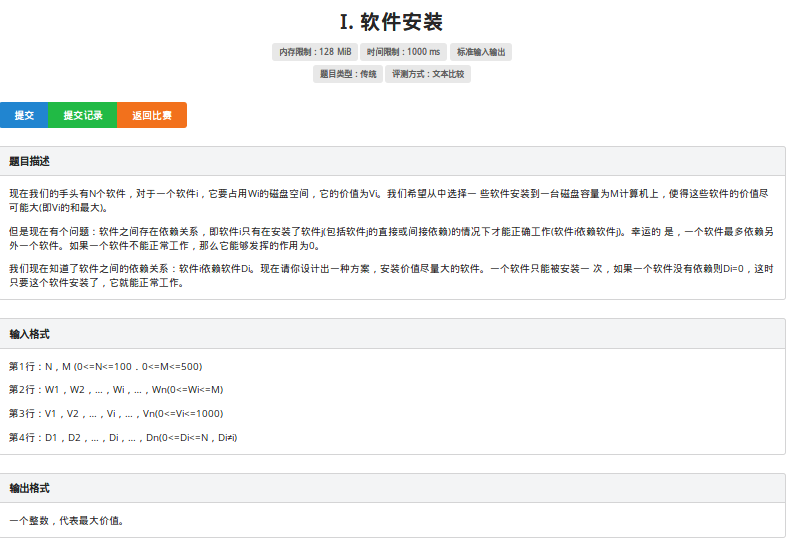
提炼：tarjan环缩成点，建0虚根，跑树形DP,最难的是看出可能有n个点n条边然后缩点，n个点n条边可能不只有一个环

n个点n条边->基环树：

基环树,也是环套树,简单地讲就是树上在加一条边。

既然成环就必定要么全选要么全不选，直接缩成一个点即可。

我的错误：

1.第二次建图时跑的第一次的邻接表

2.在读入时就建立了虚根0，但tarjan缩完后将环变成了孤点，建虚根毫无作用

结论：要在有实际意义的前提上对算法作出改进！不能有啥是啥！

Code

#include<cstdio>
using namespace std;
const int N=;
const int V=;
int n,m,rt,num_bian,num_ibian,num_huan,num_tarjan,num_que,
pw[N],pv[N],w[N],v[N],fm[N],to[N],head[N],nxt[N],ito[N],ihead[N],inxt[N],dfn[N],low[N],bel[N],que[N],in_que[N],dp[N][V],ru[N];
void add(int x,int y){
    to[++num_bian]=y,fm[num_bian]=x,nxt[num_bian]=head[x],head[x]=num_bian;
}
void iadd(int x,int y){
    ito[++num_ibian]=y,inxt[num_ibian]=ihead[x],ihead[x]=num_ibian,ru[y]++;
}
int min(int x,int y){return x>y?y:x;}
int max(int x,int y){return x>y?x:y;}
void tarjan(int x){
    dfn[x]=low[x]=++num_tarjan;
    que[++num_que]=x;in_que[x]=;
    for(int i=head[x],y;i;i=nxt[i])
        if(!dfn[y=to[i]])tarjan(y),low[x]=min(low[x],low[y]);
        else if(in_que[y])low[x]=min(low[x],dfn[y]);
    if(dfn[x]==low[x]){
        ++num_huan;
        int y;
        do{
            y=que[num_que--];
            in_que[y]=;
            bel[y]=num_huan;
        }while(y!=x);
    }
}
void dfs(int x){
    for(int i=ihead[x],y;i;i=inxt[i]){
        dfs(y=ito[i]);
        for(int j=m;j>=;--j)for(int k=j;k;--k)
            dp[x][j]=max(dp[x][j],dp[x][j-k]+dp[y][k]);
            //printf("dp[%d][%d]=%d\n",x,j,dp[x][j]);
    }
    if(v[x]!=)for(int i=m;i;--i)
        if(i>=v[x])dp[x][i]=dp[x][i-v[x]]+w[x];
        else dp[x][i]=;
}
void debug(){
    for(int i=;i<=n;++i)printf("%d ",bel[i]);puts("");
    for(int i=num_huan;i;--i)printf(":%d %d ",w[i],v[i]);puts("");
    printf("%d\n",rt);
}
int main(){
//freopen("text.in","r",stdin);
//freopen("1.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;++i)scanf("%d",&pv[i]);for(int i=;i<=n;++i)scanf("%d",&pw[i]);for(int i=,x;i<=n;++i){scanf("%d",&x);if(x)add(x,i);}
    for(int i=;i<=n;++i)if(!dfn[i])tarjan(i);
    for(int i=;i<=num_bian;++i)if(bel[fm[i]]!=bel[to[i]])iadd(bel[fm[i]],bel[to[i]]);
    for(int i=;i<=n;++i)w[bel[i]]+=pw[i],v[bel[i]]+=pv[i];
    for(int i=;i<=num_huan;++i)if(!ru[i])iadd(,i);
    dfs();
    printf("%d\n",dp[][m]);
    //debug();
    return ;
}

我还贴心的准备了对拍（Linux）代码（其实是我拍了2h呜呜呜）

#include<bits/stdc++.h>
using namespace std;
int main(){
    for(int i=;i<=;++i){
        system("./1");
        system("./2");
        system("./rand");
        if(system("diff 1.out 2.out")){
            puts("Wrong Answer");return ;
        }
        else puts("Accepted");
    }
}

pai.cpp

rand 代码

#include<bits/stdc++.h>
using namespace std;
const int N=;
int main(){
    freopen("text.in","w",stdout);
    srand((unsigned)time());
    int n=rand()%N+,m=rand()%N+;
    printf("%d %d\n",n,m);
    for(int i=;i<=n;++i){
        int v=rand()%n+;
        printf("%d ",v);
    }puts("");
    for(int i=;i<=n;++i){
        int w=rand()%n+;
        printf("%d ",w);
    }puts("");
    for(int i=,li;i<=n;++i){
        do
            li=rand()%n;
        while(li==i);
        printf("%d ",li);
    }puts("");
}

rand.cpp

注：读入text.in,正解1.cpp,输出1.out,你的错解是2.cpp,输出2.out

还不快谢谢我！