题解 P3166 【[CQOI2014]数三角形】

做完之后看了看题解，怎么一篇和我思路一样的也没有...我好慌啊qwq（所以一定是窝太弱了看不懂dalao的思路）

好吧窝的方法确实很奇怪：

核心代码只有3行 输入 循环 输出 一气呵成 是题解中的豪杰

最重要的是

没有组合数 没有容斥 没有斜率 没有向量 DA☆ZE

（只有我们的好朋友gcd

---

咳咳 那么开始正题（敲黑板）

首先，我们定义一个网格被一个三角形完全覆盖，当且仅当这个三角形的三个顶点都在网格边界上，并且沿着网格内部任意一条线段把网格切开，一定会把三角形切成两部分。比如下面的例子就是一个完全覆盖（渣鼠绘）：

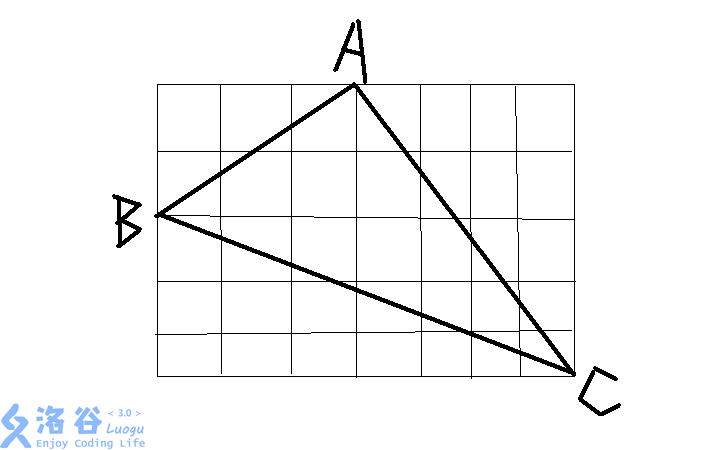
但是这个就不是：（因为沿红色竖线切开，并不能切到三角形）

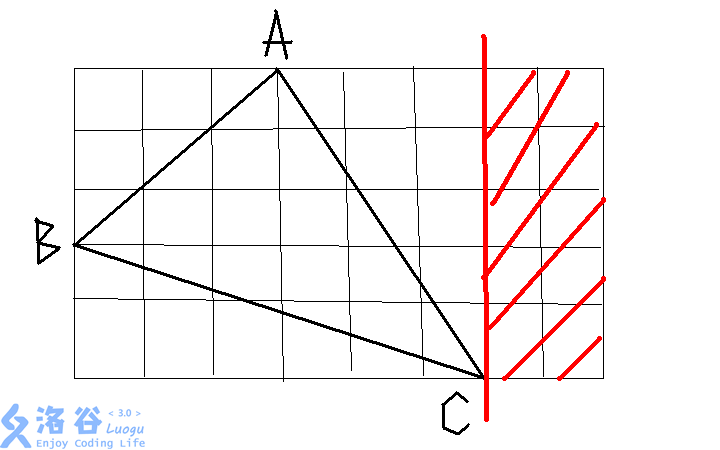
那么我们发现：

• 每个顶点都在格点上的三角形，有且只有一个可以被它完全覆盖的网格。所以只要求出原矩形当中所有子矩形的完全覆盖三角形的数量，就可以不重不漏地找出顶点都在格点上的三角形。

——但是子矩形好多啊，枚举左上角和右下角，至少是\(n^2m^2\)的数量级哇qwq

——[恋符]MasterSpark.gif 注意到我们并不关心每个子矩形的位置，而只关心它们的长宽，以及长宽均相同的矩形的数目，所以枚举子矩形的长 \(i\) 和宽 \(j\)，则\(i*j\)的矩形数量为\((n-i+1)*(m-j+1)\)，子矩阵数量级降为\(nm\)。

至此，原问题转化为 

**给定网格的长宽，迅速求解完全覆盖网格的三角形的数目**

---

继续观察，我们发现：

• 如果某个三角形（暂且称之为\(ABC\)）完全覆盖了某个网格（\(MNPQ\)），\(ABC\)一定有至少一个顶点在\(MNPQ\)的角上。

首先分析只有一个顶点在\(MNPQ\)角上的情况。不妨设\(A\)点与\(M\)点重合，为了使\(ABC\)完全覆盖\(MNPQ\)，\(B\)和\(C\)必须分别在\(NP\)和\(PQ\)边上（如下图）：

显然对于一个\(i*j\)的网格(这里\(i\) \(j\)指的是空格的数量而非格点，上图\(i=6,j=10\))，固定顶点的位置有四种，每种对应的另外两个顶点的位置有\((i-1)*(j-1)\)种(\(B\) \(C\)不能与\(N\) \(P\) \(Q\)重合)，共\(4*(i-1)*(j-1)\)种。

分析两个顶点在\(MNPQ\)角上的情况。不妨设\(A\)与\(M\)重合。此时另外一个角上的点（不妨设为点\(B\)）有三种情况：

1、\(B\)与\(N\)重合。此时\(C\)一定在\(QP\)上。共\((i-1)\)种情况。

2、\(B\)与\(Q\)重合。此时\(C\)一定在\(NP\)上。共\((j-1)\)种情况。

3、\(B\)与\(P\)重合。

这是比较麻烦的一种状态，因为此时\(C\)点可以在网格中能构成三角形的任意一处。但是我们注意到，如果线段\(AB\)除了经过\(M\) \(P\)之外，还经过了一些其他格点，\(C\)是不能与它们重合的。

那么有多少个格点被\(AB\)穿过呢qwq？

显然，不包括\(AB\)本身，有\(gcd(i,j)-1\)个（至于为什么，请读者自己思考（明明就是你自己也不会证吧kora

所以第三种情况的方案数是\((i+1)*(j+1)-4-gcd(i,j)+1\)（这里\(-4\)是因为C点不能放在网格的四个角上）。

注意到以上三种情况都可以反转，从而得到另一组与其一一对应的方案。

分析三个顶点在\(MNPQ\)角上的情况。显然只有四种。

综上，对于一个长宽为\(i,j\)的网格，可以把它完全覆盖的三角形的个数

\(S=4*(i-1)*(j-1)+2*[(i-1)+(j-1)+(i+1)*(j+1)-4-gcd(i,j)+1]+4\)

\(=6*i*j-2*gcd(i,j)\)

枚举子矩阵的复杂度为\(mn\)，单次求解\(gcd\)的复杂度为\(log(m+n)\),总复杂度\(O(mnlog(m+n))\),实际运行跑的飞起。

下面是AC代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define R register
#define ll long long
using namespace std;

int getgcd(int a, int b)
{
	if (!b) return a;
	return getgcd(b, a % b);
}

int main()
{
	ll n, m, ans = 0;
	cin >> n >> m;
	for (R int i = 1; i <= n; ++i)
		for (R int j = 1; j <= m; ++j)
			ans += (n - i + 1) * (m - j + 1) * (6 * i * j - 2 * getgcd(i, j));
	cout << ans;
	return 0;
}

那么这篇文章就到这里，希望对您能有帮助。ありがとナスます~