bzoj 2437: [Noi2011]兔兔与蛋蛋

Description

Solution

考虑犯错误的条件：之前是处于必胜状态，该操作之后就变成了必败状态.

我们可以把这个过程看成两人对网格图进行黑白染色，变成了一个二分图模型，即当前位置向相邻不同颜色的位置连边，构成的二分图，一次游戏相当于一个最大匹配.

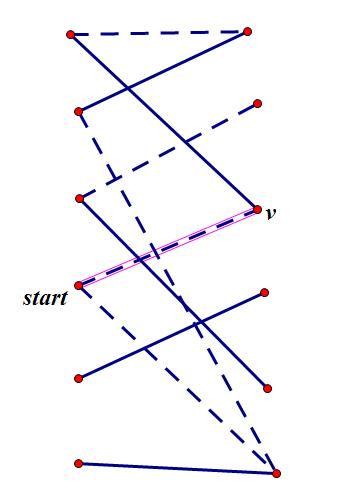
一个结论：如果一定存在包含当前位置的最大匹配，那么处于先手必胜状态

证明：

因为当前点不处于最大匹配中，那么只有非匹配边可以走，假设走到了\(v\)，\(v\)点则可以走匹配边，假设走了一条匹配边，则到达的下一个点只能走非匹配边，因为匹配的点是\(v\)， 综上：先手只能一直沿着非匹配边走，而后手有匹配边可以走，所以不是必胜状态

所以只需要判断一个点是否在一定在最大匹配中了

方法是：删除该点，再跑一次最大匹配，如果能成功匹配则不满足条件.

一个细节：一定不会存在回路，即一个点只会走一次，所以走过的点不能再进入匹配中

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#define RG register
#define il inline
#define iter iterator
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
using namespace std;
typedef long long ll;
const int N=45;
int x,y,nxt[N*N*8],to[N*N*8],num=0,w[N*N];
int n,m,a[N][N],id[N][N],cnt=0;char s[N];
bool vis[N*N],ans[N*N*2];int b[N*N],head[N*N];
void link(int x,int y){nxt[++num]=head[x];to[num]=y;head[x]=num;}
inline bool dfs(int x){
	for(int i=head[x];i;i=nxt[i]){
		int u=to[i];
		if(!vis[u] && !w[u]){
			vis[u]=1;
			if(!b[u] || dfs(b[u])){
				b[u]=x;b[x]=u;
				return true;
			}
		}
	}
	return false;
}
void build(){
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(((i+j)&1)^((x+y)&1)^(a[i][j]==1))
				id[i][j]=++cnt;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			if(!id[i][j])continue;
			if(i<n && id[i+1][j])link(id[i][j],id[i+1][j]);
			if(i>1 && id[i-1][j])link(id[i][j],id[i-1][j]);
			if(j<m && id[i][j+1])link(id[i][j],id[i][j+1]);
			if(j>1 && id[i][j-1])link(id[i][j],id[i][j-1]);
		}
}
void work()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%s",s+1);
		for(int j=1;j<=m;j++){
			if(s[j]=='X')a[i][j]=1;
			else if(s[j]=='O')a[i][j]=2;
			else x=i,y=j,a[i][j]=1;
		}
	}
	build();
	for(int i=1;i<=cnt;i++){
		if(!b[i]){
			memset(vis,0,sizeof(vis));
			dfs(i);
		}
	}
	int Q,ret=0;
	cin>>Q;
	for(int i=1;i<=Q<<1;i++){
		w[id[x][y]]=1;
		if(!b[id[x][y]])ans[i]=0;
		else{
			int u=id[x][y],v=b[u];
			b[u]=b[v]=0;
			memset(vis,0,sizeof(vis));
			ans[i]=(!dfs(v));
		}
		scanf("%d%d",&x,&y);
	}
	for(int i=1;i<=Q;i++)
		if(ans[2*i-1]&ans[i<<1])ret++;
	printf("%d\n",ret);
	for(int i=1;i<=Q;i++)
		if(ans[2*i-1]&ans[i<<1])printf("%d\n",i);
}

int main()
{
	freopen("pp.in","r",stdin);
	freopen("pp.out","w",stdout);
	work();
	return 0;
}