【学习笔记】Manacher算法

本文部分图片来源 代码来源（代码是学姐哒..

一、引入

Manacher算法是用来求最长回文子串的算法，时间复杂度O(n)。

回文子串指的是''aacaa'',''noon''，这种正着反着读都一样的。

二、构造字符串

朴素的求法是O(n^2)，以某个字符为中心，向左右扩展，如下图所示。

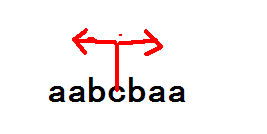
对于长度为奇数的字符串是可以枚举回文串的中心的，那么偶数的呢？

我们在字符的空里插入其他不在字符串中出现过的字符,如’#‘。

如字符串acca，变为$a#c#c#a#，为了避免出现错误，我们不让首字符等于尾字符。

所以在开头插入的字符为‘$’。

三、引进Len数组

假设输入的字符串为s。

Len[i]表示以i为中心的最长的回文半径的长度(包括i)。

如果以str[i]为中心的回文串的范围为[l,r]，那么Len[i]=r-i+1。

Len数组的性质，Len[i]-1为该回文串在原串s中的长度。

证明：2*Len[i]-1表示带’#‘的回文串的长度，’#‘的个数一共有Len[i]个，那么回文串

的长度就是2*Len[i]-1-Len[i]=Len[i]-1。

如图所示：

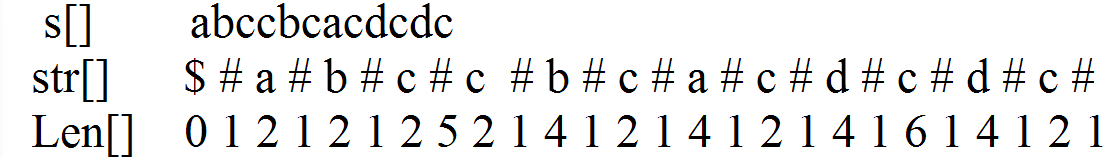
还要介绍几个变量的意义：现在从左到右扫字符串计算Len数组，mx表示目前为止的回文串能覆盖的最右端点，

id表示最后更新mx的i的位置。

四、计算Len数组

由于回文串有对称的特点，那么对于Len数组的求法，我们尽量的抄之前与该字符对称字符的Len[]。

另外，我们约定mx是开区间的，也就是说覆盖的最右端点为mx-1，这是对于下面的Manacher代码模板来约定的。

怎样通过‘抄’来计算Len数组呢？

假设现在正在计算Len[i]的值。

A：当i<mx。

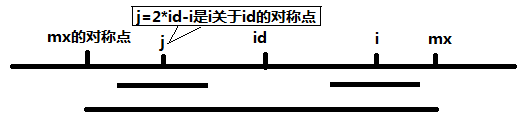
(1)：当Len[j]<=mx-i时，那么以i为中心的回文串至少和以j为中心的回文串相等。

也就是Len[i]>=Len[j],所以我们先直接抄过Len[j]赋值给Len[i],然后再暴力，看能否再扩展。

更新mx和id。

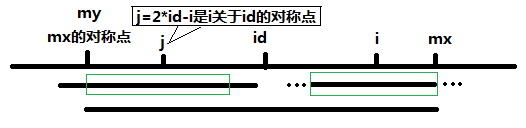
(2)：当Len[j]>mx-i时，那么i+Len[j]已经大于mx，我们对于mx向右的地方是未知的，

所以不能直接把Len[j]抄过来，只能让Len[i]先等于mx-i，这是一定对的，然后在暴力扩展。

 B：当i>=mx，也就是说Len[i]没有办法从j这里抄过来，需要暴力计算。

五、模板

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int maxn=1e6+;
char s[maxn*],str[maxn*];
int Len[maxn*],len;

void getstr()
{
    int k=;
    str[k++]='$';
    for(int i=;i<len;i++)
        str[k++]='#',
        str[k++]=s[i];
    str[k++]='#';
    len=k;
}
void Manacher()
{
    getstr();
    int mx=,id;
    for(int i=;i<len;i++)
    {
        if(mx>i) Len[i]=min(Len[*id-i],mx-i);
        else Len[i]=;
        while(str[i+Len[i]]==str[i-Len[i]])
            Len[i]++;
        if(Len[i]+i>mx)
            mx=Len[i]+i,id=i;
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%s",&s);
        len=strlen(s);
        Manacher();
        int ans=;
        for(int i=;i<len;i++) ans=max(ans,Len[i]);
        printf("%d\n",ans-);
    }
    return ;
}

模板需要注意的就是数组的大小了。

六、习题

BZOJ 2342: [Shoi2011]双倍回文

[BZOJ2565] 最长双回文串

[BZOJ3790] 神奇项链

[BZOJ2160]拉拉队排练