chcapter 11 熵和信息
Entropy and information
熵:度量一个物理系统中的态的不确定度。
注意: 文中出现的‘ 凸性’ convexity 和 ‘ 凹性’ concavity 的在不同的教材中可能含义相反。
有2个概念: 矩阵的 kernal, 和矩阵的 support
11.1 经典信息论: 香农熵
11.2 熵的基本性质
11.2.1 二元熵
11.2.2 相对熵
11.2.3 条件熵和互信息
11.2.4 数据处理不等式
11.3 冯诺依曼熵
11.3.1 量子相对熵
11.3.2 量子熵的基本性质
11.3.3 测量和熵
11.3.4 量子子可加性
11.3.5 熵的凹性
11.3.6 混合量子系统的熵
11.4 强-子可加性: 三体系统
11.1 香农熵
对于一个随机变量X,熵即可视为在知道X的值之前我们不确定度的度量,也可以度量在知道X的值之后我们获得的信息,这两种观点是互补的。
熵定义为:随机变量取不同可能值的概率的函数,而不关心具体的值是多少。
设概率分布为 p1,p2,…,pn, 则相联系的香农熵为:
H(X)=H(p1,p2,…,pn)= - ∑x px*log(px)
这样定义熵可以用来 ‘ 量化存储信息所需的资源 ’。参考 ‘ 香农无噪声编码理论 ’ 。shannon's noiseless coding theorem
例子: 假设一个信息源产生 4个符号 1,2,3,4 中的一个。无压缩时,对于源的每一次使用,对应4个可能输出的 2 bits 存储空间被占用。 假设
产生 1 的概率为 1/2 ,
产生 2 的概率为 1/4 ,
产生 3 的概率为 1/8 ,
产生 4 的概率为 1/8 。
可采用 Huffman 编码, 即利用输出的‘ 偏爱 bias’ 来压缩源。如 1 编码为 0,2 编码为 10,3 编码为 110,4 编码为 111. 则压缩串的平均长度为 7/4.
这个和源的熵相一致: H(X)=7/4
可以证明:进一步压缩源会导致数据不可恢复地损失;熵量化了可能达到的最优压缩。
上面这个例子揭示了一个信息理论的核心理念: 对信息的基本测量可解答 ‘ 解决信息处理问题所需的物理资源 ’。
11.1 熵的基本性质
11.2.1 二元熵
当p=1/2. Hmax=1
具有凹性质: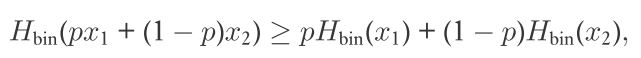 for 0<=p,x1,x2<=1
for 0<=p,x1,x2<=1
11.2.2 相对熵。
度量2个概率分布 p(x)和 q(x) 有多近。
the relative entropy of p(x) to q(x) is 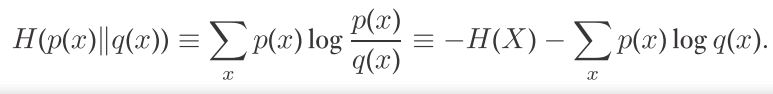
显然 相对熵是体现‘ 差异’,或者说‘ 不一样的’ 信息。如果 p(x)=q(x) ,没有差异性的信息,相对熵当然为0
非负性:相对熵总是非负的。
一些熵有关的量能被认为是相对熵的特例。
例子: 设 p(x) 为X的概率分布,有d个结果;p(x)=1/d 为均匀分布。则通过相对熵的非负性可以证明:
log d>=H(x)
香农熵的次可加性:对于二元概率分布
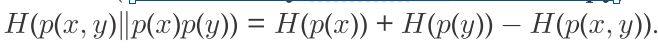
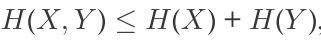
等号为当 X 和 Y 为独立随机变量时成立。
这也很好理解,当X和Y有关联时,那它们的‘ 联合信息’ 量肯定少于各自的信息量加起来。
11.2.3 条件熵和互信息。
如何表示 X中与Y有关的信息内容。
X和Y的联合熵 joint entropy 为:
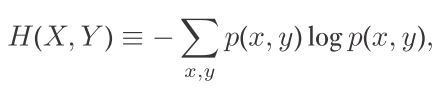
对于 pair (X,Y),假设我们知道 Y的值,剩下的不确定度与‘不知道X’ 相联系。‘ 在知道Y条件上的X的熵 ’ 定义为:
H(X|Y)=H(X,Y)-H(Y)
'X 和 Y 的互信息内容',度量X和Y有多少共同信息。

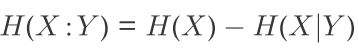


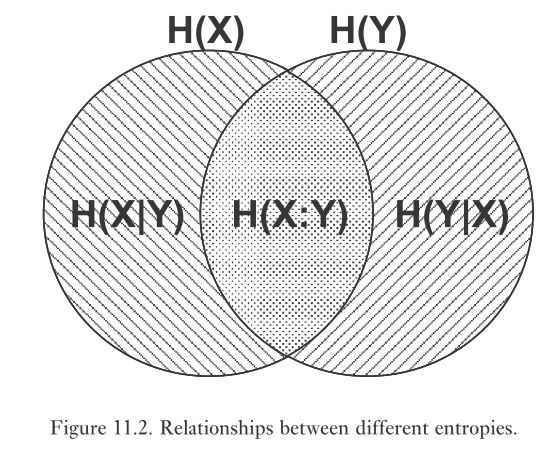
用韦恩图方便记忆:
条件熵的链式法则:
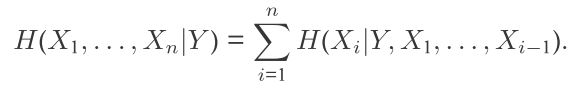
11.2.4 数据处理不等式
声明: 输出信息只能随时间减少:一旦信息丢失,就永远流失。
一个 Markov chain 是一个序列 X1->X2->…… , Xn+1 独立于 X1,…,Xn-1, 在给定 Xn 下。

11.3 冯诺依曼熵
量子态中,其密度算符取代了额经典概率分布。因此:
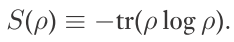

完全混合态,其熵为 log d. d 为希尔伯特空间维度
显然: 纯态的熵为0,因为纯态的本征值为 1,0,0,0……
11.3.1 量子相对熵
非负,可以是无穷大。
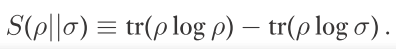
11.3.2 熵的基本性质

结论:1. 可以根据定义证明: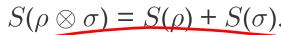
2. 对于有2部分 A 和 B 的复合量子系统, 其 ‘ 联合熵 ’ S(A,B) 定义为: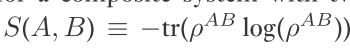
11.3.3 测量和熵
当我们对一个量子系统执行测量,其熵如何表现?
投影测量会增加熵 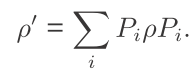
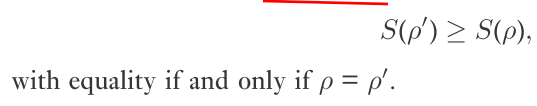
Pi 为正交投影子的完备集。
以 1-qubit 为例, 如果测量前为纯态 H,那么测量后态还为 H;
为纯态+ , 为完全混态密度矩阵。
广义测量可以减少熵: 如 |0><0|+|0><1|
11.3.4 子可加性
A和B系统的联合熵满足:
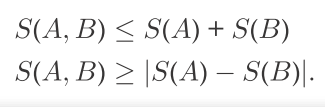
第一个式子当 A,B为分离态时取等号。
11.3.5 熵的凹性质
给定概率 pi 和密度矩阵 rou:
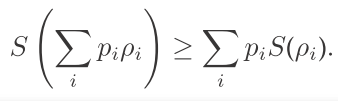
证明这个不等式用了一个技巧: 引入一个辅助系统 B。最后B的熵可以消掉。
11.3.6 混合量子态的熵
其上下界为:

11.4 强- 子可加性
3个量子系统 A,B,C 的态有:
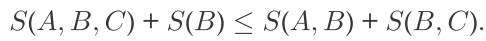
chcapter 11 熵和信息的更多相关文章
- 02-Nov-2017 07:11:56.475 信息 [http-nio-8080-exec-10] com.mchange.v2.c3p0.impl.AbstractPoolBackedDataSource. Initializing c3p0 pool...
报错: 02-Nov-2017 07:11:56.475 信息 [http-nio-8080-exec-10] com.mchange.v2.c3p0.impl.AbstractPoolBackedD ...
- 第九个知识点:香农(Shannon)定义的熵和信息是什么?
第九个知识点:香农(Shannon)定义的熵和信息是什么 这是计算机理论的最后一篇.我们讨论信息理论的基础概念,什么是香农定义的熵和信息. 信息论在1948年被Claude E.Shannon建立.信 ...
- 【视频编解码·学习笔记】11. 提取SPS信息程序
一.准备工作: 回到之前SimpleH264Analyzer程序,找到SPS信息,并对其做解析 调整项目目录结构: 修改Global.h文件中代码,添加新数据类型UINT16,之前编写的工程中,UIN ...
- C++编程规范之11:隐藏信息
摘要: 不要泄密,不要公开提供抽象的实体的内部信息. 为了尽量减少操作抽象的调用代码和抽象的实现之间的依赖性,必须隐藏实现内部的数据.否则,调用代码就能够访问该信息,或者更糟,操作该信息,而原来应属于 ...
- C#使用Xamarin开发可移植移动应用终章(11.获取设备信息与常用组件,开源一个可开发模版.)
前言 系列目录 C#使用Xamarin开发可移植移动应用目录 源码地址:https://github.com/l2999019/DemoApp 可以Star一下,随意 - - 说点什么.. 本系列,终 ...
- [机器学习]信息&熵&信息增益
关于对信息.熵.信息增益是信息论里的概念,是对数据处理的量化,这几个概念主要是在决策树里用到的概念,因为在利用特征来分类的时候会对特征选取顺序的选择,这几个概念比较抽象,我也花了好长时间去理解(自己认 ...
- ManagementClass类解析和C#如何获取硬件的相关信息
在.NET的项目中,有时候需要获取计算机的硬件的相关信息,在C#语言中需要利用ManagementClass这个类来进行相关操作. 现在先来介绍一下ManagementClass类,首先看一下类的继承 ...
- SQL Server安全(11/11):审核(Auditing)
在保密你的服务器和数据,防备当前复杂的攻击,SQL Server有你需要的一切.但在你能有效使用这些安全功能前,你需要理解你面对的威胁和一些基本的安全概念.这篇文章提供了基础,因此你可以对SQL Se ...
- shopnc2014年11版数据库字典
shopnc_activity 表注释: 活动表 字段 类型 空 默认 注释 activity_id mediumint(9) 否 id activity_title varchar(255) 否 ...
- 解决安装失败的 Internet Explorer 11
注意:这篇文章是由无人工介入的微软自动的机器翻译软件翻译完成.微软很高兴能同时提供给您由人工翻译的和由机器翻译的文章, 以使您能使用您的语言访问所有的知识库文章.然而由机器翻译的文章并不总是完美的.它 ...
随机推荐
- WPF使用Grid布局
WPF布局 WPF布局基础 布局原则 一个窗口中只能包含一个元素 不应显示设置元素尺寸 不应使用坐标设置元素的位置 可以嵌套布局容器 布局容器 StackPanel: 水平或垂直排列元素.Orient ...
- Win32 API 读取文件
昨天又用Win32来读取文件的时候,又出现了字符编码的问题. 用TCHAR字符来写文件呢,用系统的记事本打开是乱码. 用CHAR字字符来写呢,在读取汉字的时候后面有一串乱码, 用CHAR[]数组读取就 ...
- 强!34.1K star! 再见Postman,新一代API测试利器,功能强大、颜值爆表!
1.引言 在当今的互联网时代,API(应用程序编程接口)已经成为连接不同软件系统的桥梁.作为一名开发者,掌握API测试技能至关重要.市面上的API测试工具琳琅满目,今天我们要介绍的是一款开源.跨平台的 ...
- 卡农 -- HNOI2011 -- DP&组合
卡农 -- \(HNOI2011\) $$luogu$$ $$HZOI$$ 题意 给定一个 集合 $ A= { 1 \le x \le n | x } $ , 求出其 \(m\) 个不相同的且不为空集 ...
- 【Mac】之安装FileZilla
FileZilla下载地址:http://www.pc6.com/mac/111230.html 连接FTP服务器: 下载完成之后需要修改字符集编码: ①先添加站点 ②填写:gb2312字符集
- 基于 Quanto 和 Diffusers 的内存高效 transformer 扩散模型
过去的几个月,我们目睹了使用基于 transformer 模型作为扩散模型的主干网络来进行高分辨率文生图 (text-to-image,T2I) 的趋势.和一开始的许多扩散模型普遍使用 UNet 架构 ...
- OpenFeign深入学习笔记
OpenFeign 是一个声明式的 Web 服务客户端,它使得编写 Web 服务客户端变得更加容易.OpenFeign 是在 Spring Cloud 生态系统中的一个组件,它整合了 Ribbon(客 ...
- 【YashanDB知识库】outline固化执行计划
[问题分类]性能优化,功能使用 [关键字]outline [问题描述]防止SQL执行计划突变,用outline固化执行计划 [问题原因分析]防止SQL执行计划突变,用outline固化执行计划 [解决 ...
- 推荐一款开源、高效、灵活的Redis桌面管理工具:Tiny RDM!支持调试与分析功能!
1.引言 在大数据和云计算快速发展的今天,Redis作为一款高性能的内存键值存储系统,在数据缓存.实时计算.消息队列等领域发挥着重要作用.然而,随着Redis集群规模的扩大和复杂度的增加,如何高效地管 ...
- spark 自定义 accumulator
默认的accumulator 只是最简单的 int/float 有时候我需要一个map来作为accumulator 这样,就可以处理 <string, int>类型的计数了. 此外我还需要 ...
