我理解的数据结构（二）—— 栈（Stack）

我理解的数据结构（二）—— 栈（Stack）

一、栈基础

• 栈是一种线性结构
• 相比较数组，栈对应的操作是数组的子集
• 只能从一端添加元素，也只能从同一端取出元素，这一端称为栈顶
• 栈是一种后进先出的数据结构，LIFO（Last In First Out）

二、栈的应用

• Undo操作（撤销）
• 程序调用所使用的系统栈

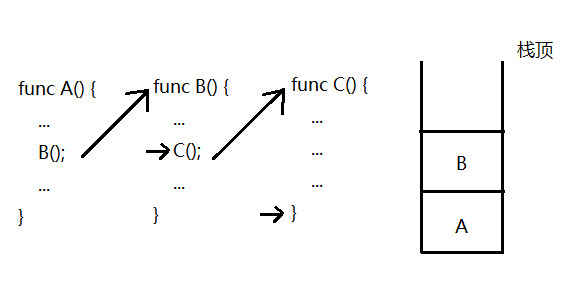
三、栈的实现

其实，实现一个栈结构非常简单，我们只需要复用上一节我们自己封装的数组就可以快速的实现一个栈的创建。
以数组的最后一个元素当成栈顶元素。

1. 首先，我们先创建一个栈的借口，里面声明我们需要实现的方法：

```
public interface Stack<E> {
boolean isEmpty();
int getSize();
// 移除栈顶元素
E pop();
// 查看栈顶元素
E peek();
// 压入栈
void push(E ele);
}
```

注：这里我们有一个peek方法，就是查看栈顶元素，所以我们需要给我们自己封装的数组类添加一个查看最后一个元素的方法：

```
// 获取最后一个元素
public E getLast() {
return get(size - 1);
}
```

2. 封装我们自己的栈

```
public class ArrayStack<E> implements Stack<E> {

private ArrayNew<E> array;

public ArrayStack(int capacity) {
    array = new ArrayNew<>(capacity);
}

public ArrayStack() {
    array = new ArrayNew<>();
}

public int getCapacity() {
    return array.getCapacity();
}

@Override
public int getSize() {
    return array.getSize();
}

@Override
public boolean isEmpty() {
    return array.isEmpty();
}

@Override
public void push(E ele) {
    array.addLast(ele);
}

@Override
public E pop() {
    return array.removeLast();
}

@Override
public E peek() {
    return array.getLast();
}

@Override
public String toString() {
    StringBuilder res = new StringBuilder();

    res.append("Stack: [");
    for (int i = 0; i < getSize(); i++) {
        res.append(array.get(i));
        if (getSize() - 1 != i) {
            res.append(", ");
        }
    }
    res.append("] top");
    return res.toString();
}

}

<p><strong>注：</strong>其中的<code>ArrayNew</code>即是我们在上一节自己封装的数组类，不知道的同学可以去查看：<br><a href="https://segmentfault.com/a/1190000016064569">我理解的数据结构（一）—— 不要小看了数组</a></p>
<blockquote>因为我在<code>ArrayNew</code>中已经实现了动态数组，所以不用考虑栈长度的问题，这样我们就自己封装了一个栈（注释在<code>Stack</code>接口中和<code>ArrayNew</code>类中足够详细）。</blockquote>
<h3>四、用栈去解决《有效的括号》</h3>
<blockquote>这是一道<code>leetcode</code>上，编号为20的题目，具体题目描述如下：</blockquote>

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

1.左括号必须用相同类型的右括号闭合。

2.左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

<p><strong>解题思路</strong></p>
<ol>
<li>首先，我们可以把左括号直接压入栈，不论是小括号、中括号还是大括号。</li>
<li>
<p>如果拿到的是右括号，则需要做匹配判断。</p>
<ul>
<li>拿出栈顶元素，如果与之右括号匹配，则<code>pop</code>出栈顶元素。</li>
<li>拿出栈顶元素，如果与之右括号不匹配，则返回<code>false</code>。</li>
</ul>
</li>
<li>
<p>如果字符串比较完成，没有返回<code>false</code>，则判断栈是否为空。</p>
<ul>
<li>为空，返回<code>true</code>，括号匹配成功</li>
<li>不为空，返回<code>false</code>
</li>
</ul>
</li>
</ol>
<h4>解题代码如下：</h4>

public boolean isValid(String s) {

ArrayStack<Character> stack = new ArrayStack<>();

for (int i = 0; i < s.length(); i++) {

    char c = s.charAt(i);

    // 左括号直接压入栈
    if (c == '(' || c == '[' || c == '{') {
        stack.push(c);
    } else {

        if (stack.isEmpty()) {
            return false;
        }

        char topChar = stack.pop();
        if (c == ')' && topChar != '(') {
            return false;
        }
        if (c == ']' && topChar != '[') {
            return false;
        }
        if (c == '}' && topChar != '{') {
            return false;
        }
    }

}

return stack.isEmpty();

}

<h3>五、栈的复杂度分析</h3>
<table>
<thead><tr>
<th align="center">方法</th>
<th align="center">复杂度</th>
</tr></thead>
<tbody>
<tr>
<td align="center">push</td>
<td align="center">O(1) 均摊</td>
</tr>
<tr>
<td align="center">pop</td>
<td align="center">O(1) 均摊</td>
</tr>
<tr>
<td align="center">peek</td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center">getSize</td>
<td align="center">O(1)</td>
</tr>
<tr>
<td align="center">isEmpty</td>
<td align="center">O(1)</td>
</tr>
</tbody>
</table>
<blockquote>因为栈的时间复杂度都是<code>O(1)</code>，所以栈的性能是很高的。</blockquote>

原文地址：https://segmentfault.com/a/1190000016067831