一：一般K均值聚类算法实现

（一）导入数据

import numpy as np

import matplotlib.pyplot as plt

def loadDataSet(filename):

    dataSet = np.loadtxt(filename)

    return dataSet

（二）计算两个向量之间的距离

def distEclud(vecA,vecB):   #计算两个向量之间距离

    return np.sqrt(np.sum(np.power(vecA-vecB,)))

（三）随机初始化聚簇中心

def randCent(data_X,k):    #随机初始化聚簇中心 可以随机选取样本点，或者选取距离随机

    m,n = data_X.shape

    centroids = np.zeros((k,n))

    #开始随机初始化

    for i in range(n):

        Xmin = np.min(data_X[:,i])   #获取该特征最小值

        Xmax = np.max(data_X[:,i])   #获取该特征最大值

        disc = Xmax - Xmin  #获取差值

        centroids[:,i] = (Xmin + np.random.rand(k,)*disc).flatten() #为i列特征全部k个聚簇中心赋值  rand(k,)表示产生k行1列在0-1之间的随机数

    return centroids

（四）实现聚簇算法

def kMeans(data_X,k,distCalc=distEclud,createCent=randCent):   #实现k均值算法,当所有中心不再改变时退出

    m,n = data_X.shape

    centroids = createCent(data_X,k)    #创建随机聚簇中心

    clusterAssment = np.zeros((m,))    #创建各个样本点的分类和位置信息    第一个表示属于哪一个聚簇，第二个表示距离该聚簇的位置

    changeFlag = True   #设置标识符，表示是否有聚簇中心改变

    while changeFlag:

        changeFlag = False

        #开始计算各个点到聚簇中心距离，进行点集合分类

        for i in range(m):  #对于每一个样本点，判断是属于哪一个聚簇

            bestMinIdx = -

            bestMinDist = np.inf

            for j in range(k):  #求取到各个聚簇中心的距离

                dist = distCalc(centroids[j], data_X[i])

                if dist < bestMinDist:

                    bestMinIdx = j

                    bestMinDist = dist

            if clusterAssment[i,] != bestMinIdx:   #该样本点有改变聚簇中心

                changeFlag = True

            clusterAssment[i,:] = bestMinIdx,bestMinDist

        #开始根据上面样本点分类信息，进行聚簇中心重新分配

        for i in range(k):

            centroids[i] = np.mean(data_X[np.where(clusterAssment[:,]==i)],)

    return centroids,clusterAssment

（五）结果测试

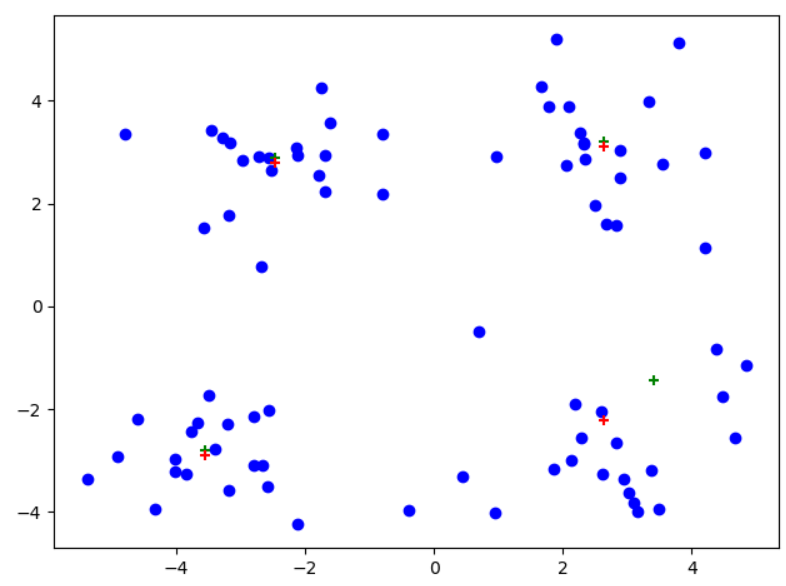
data_X = loadDataSet("testSet.txt")

centroids,clusterAssment = kMeans(data_X,)

plt.figure()

plt.scatter(data_X[:,].flatten(),data_X[:,].flatten(),c="b",marker="o")

plt.scatter(centroids[:,].flatten(),centroids[:,].flatten(),c='r',marker="+")

plt.show()

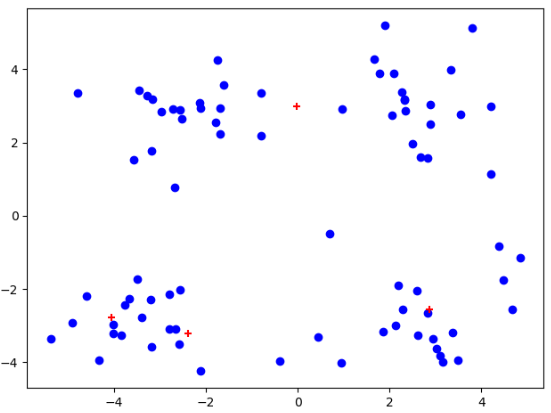
我们可以发现，在经过多次测试后，会出现聚簇收敛到局部最小值。导致不能得到我们想要的聚簇结果！！！

二：多次测试，计算代价，选取最优聚簇中心

https://www.cnblogs.com/ssyfj/p/12966305.html

避免局部最优：如果想让找到最优可能的聚类，可以尝试多次随机初始化，以此来保证能够得到一个足够好的结果，选取代价最小的一个也就是代价函数J最小的。事实证明，在聚类数K较小的情况下（2~10个），使用多次随机初始化会有较大的影响，而如果K很大的情况，多次随机初始化可能并不会有太大效果

三：后处理提高聚类性能（可以不实现）

理解思路即可，实现没必要，因为后面的二分K-均值算法更加好。这里的思路可以用到二分K-均值算法中。

通过SSE指标（误差平方和）来度量聚类效果，是根据各个样本点到对应聚簇中心聚类来计算的。SSE越小表示数据点越接近质心，聚类效果越好。

一种好的方法是通过增加聚簇中心（是将具有最大SSE值的簇划分为两个簇）来减少SSE值，但是违背了K-均值思想（自行增加了聚簇数量），但是我们可以在后面进行处理，合并两个最接近的聚簇中心，从而达到保持聚簇中心数量不变，但是降低SSE值的情况，获取全局最优聚簇中心。

（一）全部代码

import numpy as np

import matplotlib.pyplot as plt

def loadDataSet(filename):

    dataSet = np.loadtxt(filename)

    return dataSet

def distEclud(vecA,vecB):   #计算两个向量之间距离

    return np.sqrt(np.sum(np.power(vecA-vecB,)))

def randCent(data_X,k):    #随机初始化聚簇中心 可以随机选取样本点，或者选取距离随机

    m,n = data_X.shape

    centroids = np.zeros((k,n))

    #开始随机初始化

    for i in range(n):

        Xmin = np.min(data_X[:,i])   #获取该特征最小值

        Xmax = np.max(data_X[:,i])   #获取该特征最大值

        disc = Xmax - Xmin  #获取差值

        centroids[:,i] = (Xmin + np.random.rand(k,)*disc).flatten() #为i列特征全部k个聚簇中心赋值  rand(k,)表示产生k行1列在0-1之间的随机数

    return centroids

def getSSE(clusterAssment):    #传入一个聚簇中心和对应的距离数据集

    return np.sum(clusterAssment[:,])

def kMeans(data_X,k,distCalc=distEclud,createCent=randCent,divide=False):   #实现k均值算法,当所有中心不再改变时退出

    m,n = data_X.shape

    centroids = createCent(data_X,k)    #创建随机聚簇中心

    clusterAssment = np.zeros((m,))    #创建各个样本点的分类和位置信息    第一个表示属于哪一个聚簇，第二个表示距离该聚簇的位置

    changeFlag = True   #设置标识符，表示是否有聚簇中心改变

    while changeFlag:

        changeFlag = False

        #开始计算各个点到聚簇中心距离，进行点集合分类

        for i in range(m):  #对于每一个样本点，判断是属于哪一个聚簇

            bestMinIdx = -

            bestMinDist = np.inf

            for j in range(k):  #求取到各个聚簇中心的距离

                dist = distCalc(centroids[j], data_X[i])

                if dist < bestMinDist:

                    bestMinIdx = j

                    bestMinDist = dist

            if clusterAssment[i,] != bestMinIdx:   #该样本点有改变聚簇中心

                changeFlag = True

            clusterAssment[i,:] = bestMinIdx,bestMinDist

        #开始根据上面样本点分类信息，进行聚簇中心重新分配

        for i in range(k):

            centroids[i] = np.mean(data_X[np.where(clusterAssment[:,]==i)],)

    midCentroids = centroids

    #进行后处理

    if divide == True:  # 开始进行一次后处理

        maxSSE =

        maxIdx = -

        for i in range(k):  #先找到最大的那个簇，进行划分

            curSSE = getSSE(clusterAssment[np.where(clusterAssment[:,]==i)])

            if curSSE > maxSSE:

                maxSSE = curSSE

                maxIdx = i

        #将最大簇划分为两个簇

        temp,new_centroids,new_clusterAssment = kMeans(data_X[np.where(clusterAssment[:,]==maxIdx)],)

        centroids[maxIdx] = new_centroids[]    #更新一个

        centroids = np.r_[centroids,np.array([new_centroids[]])]   #更新第二个

        new_clusterAssment[,:] = maxIdx

        new_clusterAssment[,:] = centroids.shape[] - 

        #找的最近的两个聚簇中心进行合并

        clusterAssment[np.where(clusterAssment[:,]==maxIdx)] = new_clusterAssment  #距离更新

        distArr = np.zeros((k+,k+))

        for i in range(k+):

            temp_disc = np.sum(np.power(centroids[i] - centroids,),)  #获取L2范式距离平方

            temp_disc[i] = np.inf   #将对角线的0值设置为无穷大，方便后面求取最小值

            distArr[i] = temp_disc

        #获取最小距离位置

        idx = np.argmin(distArr)

        cluidx = int((idx) / (k+)),(idx) % (k+)    #获取行列索引

        #计算两个聚簇的新的聚簇中心

        new_centroids = np.mean(data_X[np.where((clusterAssment[:, ] == cluidx[]) | (clusterAssment[:, ] == cluidx[]))], )

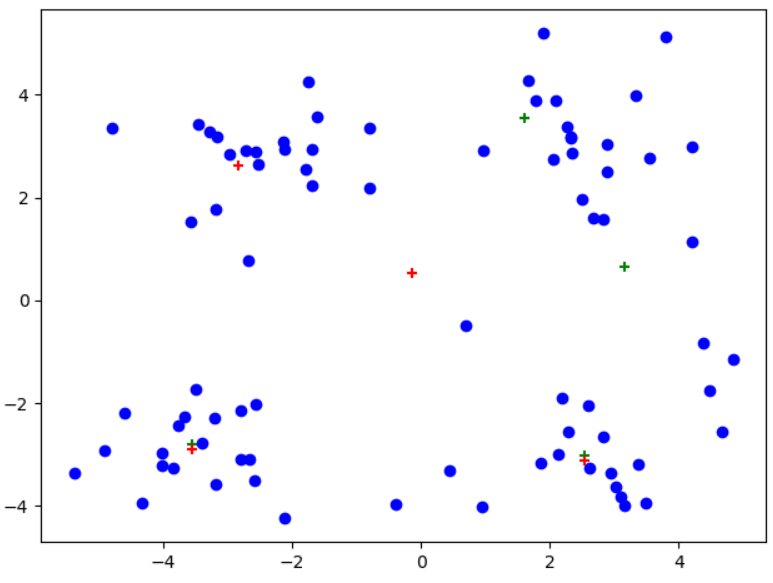
        centroids = np.delete(centroids,list(cluidx),)

        centroids = np.r_[centroids,np.array([new_centroids])]

    return midCentroids,centroids,clusterAssment

plt.figure()

data_X = loadDataSet("testSet.txt")

midCentroids,centroids,clusterAssment = kMeans(data_X,,divide=True)

midCentroids[:, ] += 0.1

plt.scatter(data_X[:,].flatten(),data_X[:,].flatten(),c="b",marker="o")

plt.scatter(midCentroids[:, ].flatten(), midCentroids[:, ].flatten(), c='g', marker="+")

plt.scatter(centroids[:,].flatten(),centroids[:,].flatten(),c='r',marker="+")

plt.show()

（二）计算SSE函数

def getSSE(clusterAssment):    #传入一个聚簇中心和对应的距离数据集

    return np.sum(clusterAssment[:,])

（三）修改原有的k-均值算法

def kMeans(data_X,k,distCalc=distEclud,createCent=randCent,divide=False):   #实现k均值算法,当所有中心不再改变时退出　　最后一个参数，用来表示是否是后处理，True不需要后处理

    m,n = data_X.shape

    centroids = createCent(data_X,k)    #创建随机聚簇中心

    clusterAssment = np.zeros((m,))    #创建各个样本点的分类和位置信息    第一个表示属于哪一个聚簇，第二个表示距离该聚簇的位置

    changeFlag = True   #设置标识符，表示是否有聚簇中心改变

    while changeFlag:

        changeFlag = False

        #开始计算各个点到聚簇中心距离，进行点集合分类

        for i in range(m):  #对于每一个样本点，判断是属于哪一个聚簇

            bestMinIdx = -

            bestMinDist = np.inf

            for j in range(k):  #求取到各个聚簇中心的距离

                dist = distCalc(centroids[j], data_X[i])

                if dist < bestMinDist:

                    bestMinIdx = j

                    bestMinDist = dist

            if clusterAssment[i,] != bestMinIdx:   #该样本点有改变聚簇中心

                changeFlag = True

            clusterAssment[i,:] = bestMinIdx,bestMinDist

        #开始根据上面样本点分类信息，进行聚簇中心重新分配

        for i in range(k):

            centroids[i] = np.mean(data_X[np.where(clusterAssment[:,]==i)],)

    midCentroids = centroids

    #进行后处理

    if divide == True:  # 开始进行一次后处理

        maxSSE =

        maxIdx = -

        for i in range(k):  #先找到最大的那个簇，进行划分

            curSSE = getSSE(clusterAssment[np.where(clusterAssment[:,]==i)])

            if curSSE > maxSSE:

                maxSSE = curSSE

                maxIdx = i

        #将最大簇划分为两个簇

        temp,new_centroids,new_clusterAssment = kMeans(data_X[np.where(clusterAssment[:,]==maxIdx)],)

        centroids[maxIdx] = new_centroids[]    #更新一个

        centroids = np.r_[centroids,np.array([new_centroids[]])]   #更新第二个

        new_clusterAssment[,:] = maxIdx

        new_clusterAssment[,:] = centroids.shape[] - 

        #找的最近的两个聚簇中心进行合并

        clusterAssment[np.where(clusterAssment[:,]==maxIdx)] = new_clusterAssment  #距离更新

        distArr = np.zeros((k+,k+))

        for i in range(k+):

            temp_disc = np.sum(np.power(centroids[i] - centroids,),)  #获取L2范式距离平方

            temp_disc[i] = np.inf   #将对角线的0值设置为无穷大，方便后面求取最小值

            distArr[i] = temp_disc

        #获取最小距离位置

        idx = np.argmin(distArr)

        cluidx = int((idx) / (k+)),(idx) % (k+)    #获取行列索引

        #计算两个聚簇的新的聚簇中心

        new_centroids = np.mean(data_X[np.where((clusterAssment[:, ] == cluidx[]) | (clusterAssment[:, ] == cluidx[]))], )

        centroids = np.delete(centroids,list(cluidx),)

        centroids = np.r_[centroids,np.array([new_centroids])]

    return midCentroids,centroids,clusterAssment　　#第一个返回的是正常k-均值聚簇结果，第二、三返回的是后处理以后的聚簇中心和样本分类信息

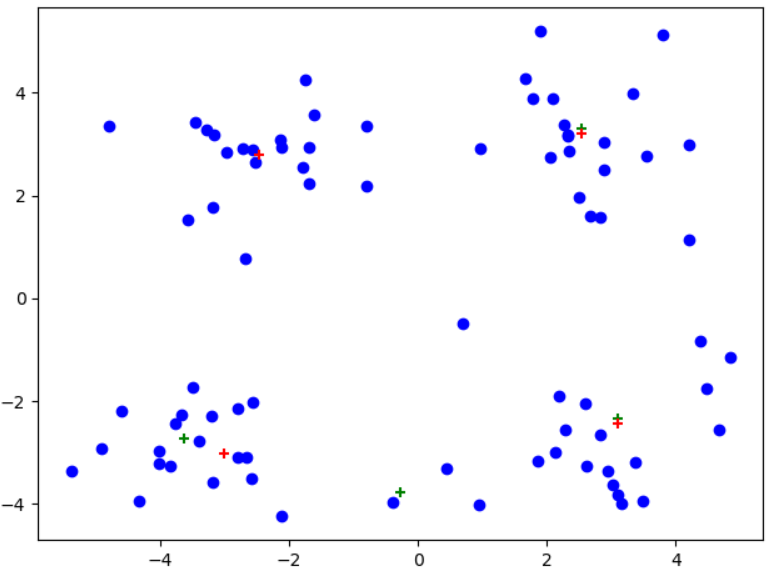
（四）测试现象

plt.figure()

data_X = loadDataSet("testSet.txt")

midCentroids,centroids,clusterAssment = kMeans(data_X,4,divide=True)

midCentroids[:, 1] += 0.1　　#将两个K-均值处理结果错开

plt.scatter(data_X[:,0].flatten(),data_X[:,1].flatten(),c="b",marker="o")　　#原始数据

plt.scatter(midCentroids[:, 0].flatten(), midCentroids[:, 1].flatten(), c='g', marker="+")　　#一般K-均值聚簇

plt.scatter(centroids[:,0].flatten(),centroids[:,1].flatten(),c='r',marker="+")　　#后处理以后的聚簇现象

plt.show()

注意：红色为后处理结果、绿色为一般K-均值处理

可以看到从左到右，后处理现象依次显现，尤其是最右边图中，后处理对原始聚簇划分进行了很大的改进！！！

虽然后处理不错，但是后面的二分K-均值算法是在聚簇时，直接考虑了SSE来进行划分K个聚簇，而不是在聚簇后进行考虑再进行划分合并。所以下面来看二分K-均值算法

四：二分K-均值算法

（一）全部代码

import numpy as np

from numpy import *

import matplotlib.pyplot as plt

def loadDataSet(filename):

    dataSet = np.loadtxt(filename)

    return dataSet

def distEclud(vecA,vecB):   #计算两个向量之间距离

    return np.sqrt(np.sum(np.power(vecA-vecB,)))

def randCent(data_X,k):    #随机初始化聚簇中心 可以随机选取样本点，或者选取距离随机

    m,n = data_X.shape

    centroids = np.zeros((k,n))

    #开始随机初始化

    for i in range(n):

        Xmin = np.min(data_X[:,i])   #获取该特征最小值

        Xmax = np.max(data_X[:,i])   #获取该特征最大值

        disc = Xmax - Xmin  #获取差值

        centroids[:,i] = (Xmin + np.random.rand(k,)*disc).flatten() #为i列特征全部k个聚簇中心赋值  rand(k,)表示产生k行1列在0-1之间的随机数

    return centroids

def kMeans(data_X,k,distCalc=distEclud,createCent=randCent):   #实现k均值算法,当所有中心不再改变时退出

    m,n = data_X.shape

    centroids = createCent(data_X,k)    #创建随机聚簇中心

    clusterAssment = np.zeros((m,))    #创建各个样本点的分类和位置信息    第一个表示属于哪一个聚簇，第二个表示距离该聚簇的位置

    changeFlag = True   #设置标识符，表示是否有聚簇中心改变

    while changeFlag:

        changeFlag = False

        #开始计算各个点到聚簇中心距离，进行点集合分类

        for i in range(m):  #对于每一个样本点，判断是属于哪一个聚簇

            bestMinIdx = -

            bestMinDist = np.inf

            for j in range(k):  #求取到各个聚簇中心的距离

                dist = distCalc(centroids[j], data_X[i])

                if dist < bestMinDist:

                    bestMinIdx = j

                    bestMinDist = dist

            if clusterAssment[i,] != bestMinIdx:   #该样本点有改变聚簇中心

                changeFlag = True

            clusterAssment[i,:] = bestMinIdx,bestMinDist

        #开始根据上面样本点分类信息，进行聚簇中心重新分配

        for i in range(k):

            centroids[i] = np.mean(data_X[np.where(clusterAssment[:,]==i)],)

    return centroids,clusterAssment

def binkMeans(data_X,k,distCalc=distEclud):   #实现二分-k均值算法，开始都是属于一个聚簇，当我们聚簇中心数为K时，退出

    m,n = data_X.shape

    clusterAssment = np.zeros((m,))

    centroid0 = np.mean(data_X,).tolist()   #全部数据集属于一个聚簇时，设置中心为均值即可

    centList = [centroid0]  #用于统计所有的聚簇中心

    for i in range(m):

        clusterAssment[i,] = distCalc(data_X[i],centroid0)#设置距离，前面初始为0，设置了聚簇中心类别

    while len(centList) < k:    #不满足K个聚簇，则一直进行分类

        lowestSSE = np.inf  #用于计算每个聚簇的SSE值

        for i in range(len(centList)): #尝试对每一个聚簇进行一次划分，看哪一个簇划分后所有簇的SSE最小

            #先对该簇进行划分，然后获取划分后的SSE值，和没有进行划分的数据集的SSE值

            #先进行数据划分

            splitClusData = data_X[np.where(clusterAssment[:, ] == i)]

            #进行簇划分

            splitCentroids,splitClustArr = kMeans(splitClusData,,distCalc)

            #获取全部SSE值

            splitSSE = np.sum(splitClustArr[:,])

            noSplitSSE = np.sum(clusterAssment[np.where(clusterAssment[:, ] != i),])

            if (splitSSE + noSplitSSE) < lowestSSE:

                lowestSSE = splitSSE + noSplitSSE

                bestSplitClus = i

                #记录划分信息

                bestSplitCent = splitCentroids

                bestSplitClu = splitClustArr.copy()

        #更新簇的分配结果 二分后数据集：对于索引0，则保持原有的i位置，对于索引1则加到列表后面

        bestSplitClu[np.where(bestSplitClu[:,]==)[],] = len(centList)

        bestSplitClu[np.where(bestSplitClu[:,]==)[],] = bestSplitClus

        #还要继续更新聚簇中心

        centList[bestSplitClus] = bestSplitCent[].tolist()

        centList.append(bestSplitCent[].tolist())

        #还要对划分的数据集进行标签更新

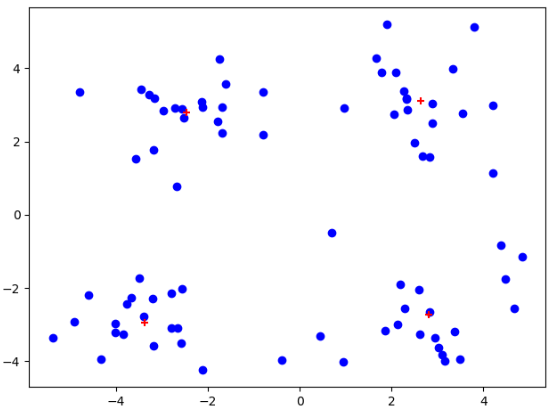
        clusterAssment[np.where(clusterAssment[:,]==bestSplitClus)[],:] = bestSplitClu

    return np.array(centList),clusterAssment

data_X = loadDataSet("testSet2.txt")

centroids,clusterAssment = binkMeans(data_X,)

plt.figure()

plt.scatter(data_X[:,].flatten(),data_X[:,].flatten(),c="b",marker="o")

print(centroids)

plt.scatter(centroids[:,].reshape(,).tolist()[],centroids[:,].reshape(,).tolist()[],c='r',marker="+")

plt.show()

（二）不变代码

import numpy as np

from numpy import *

import matplotlib.pyplot as plt

def loadDataSet(filename):

    dataSet = np.loadtxt(filename)

    return dataSet

def distEclud(vecA,vecB):   #计算两个向量之间距离

    return np.sqrt(np.sum(np.power(vecA-vecB,)))

def randCent(data_X,k):    #随机初始化聚簇中心 可以随机选取样本点，或者选取距离随机

    m,n = data_X.shape

    centroids = np.zeros((k,n))

    #开始随机初始化

    for i in range(n):

        Xmin = np.min(data_X[:,i])   #获取该特征最小值

        Xmax = np.max(data_X[:,i])   #获取该特征最大值

        disc = Xmax - Xmin  #获取差值

        centroids[:,i] = (Xmin + np.random.rand(k,)*disc).flatten() #为i列特征全部k个聚簇中心赋值  rand(k,)表示产生k行1列在0-1之间的随机数

    return centroids

def kMeans(data_X,k,distCalc=distEclud,createCent=randCent):   #实现k均值算法,当所有中心不再改变时退出

    m,n = data_X.shape

    centroids = createCent(data_X,k)    #创建随机聚簇中心

    clusterAssment = np.zeros((m,))    #创建各个样本点的分类和位置信息    第一个表示属于哪一个聚簇，第二个表示距离该聚簇的位置

    changeFlag = True   #设置标识符，表示是否有聚簇中心改变

    while changeFlag:

        changeFlag = False

        #开始计算各个点到聚簇中心距离，进行点集合分类

        for i in range(m):  #对于每一个样本点，判断是属于哪一个聚簇

            bestMinIdx = -

            bestMinDist = np.inf

            for j in range(k):  #求取到各个聚簇中心的距离

                dist = distCalc(centroids[j], data_X[i])

                if dist < bestMinDist:

                    bestMinIdx = j

                    bestMinDist = dist

            if clusterAssment[i,] != bestMinIdx:   #该样本点有改变聚簇中心

                changeFlag = True

            clusterAssment[i,:] = bestMinIdx,bestMinDist

        #开始根据上面样本点分类信息，进行聚簇中心重新分配

        for i in range(k):

            centroids[i] = np.mean(data_X[np.where(clusterAssment[:,]==i)],)

    return centroids,clusterAssment

（三）二分K-均值实现

def binkMeans(data_X,k,distCalc=distEclud):   #实现二分-k均值算法，开始都是属于一个聚簇，当我们聚簇中心数为K时，退出

    m,n = data_X.shape

    clusterAssment = np.zeros((m,))

    centroid0 = np.mean(data_X,).tolist()   #全部数据集属于一个聚簇时，设置中心为均值即可

    centList = [centroid0]  #用于统计所有的聚簇中心

    for i in range(m):

        clusterAssment[i,] = distCalc(data_X[i],centroid0)#设置距离，前面初始为0，设置了聚簇中心类别

    while len(centList) < k:    #不满足K个聚簇，则一直进行分类

        lowestSSE = np.inf  #用于计算每个聚簇的SSE值

        for i in range(len(centList)): #尝试对每一个聚簇进行一次划分，看哪一个簇划分后所有簇的SSE最小

            #先对该簇进行划分，然后获取划分后的SSE值，和没有进行划分的数据集的SSE值

            #先进行数据划分

            splitClusData = data_X[np.where(clusterAssment[:, ] == i)]

            #进行簇划分

            splitCentroids,splitClustArr = kMeans(splitClusData,,distCalc)

            #获取全部SSE值

            splitSSE = np.sum(splitClustArr[:,])

            noSplitSSE = np.sum(clusterAssment[np.where(clusterAssment[:, ] != i),])

            if (splitSSE + noSplitSSE) < lowestSSE:

                lowestSSE = splitSSE + noSplitSSE

                bestSplitClus = i

                #记录划分信息

                bestSplitCent = splitCentroids

                bestSplitClu = splitClustArr.copy()

        #更新簇的分配结果 二分后数据集：对于索引0，则保持原有的i位置，对于索引1则加到列表后面

        bestSplitClu[np.where(bestSplitClu[:,0]==1)[0],0] = len(centList)

        bestSplitClu[np.where(bestSplitClu[:,0]==0)[0],0] = bestSplitClus



        #还要继续更新聚簇中心

        centList[bestSplitClus] = bestSplitCent[].tolist()

        centList.append(bestSplitCent[].tolist())

        #还要对划分的数据集进行标签更新

        clusterAssment[np.where(clusterAssment[:,0]==bestSplitClus)[0],:] = bestSplitClu

    return np.array(centList),clusterAssment

重点：使用np.where查找时，对数据集列值进行修改时，需要选取np.where()[0]---表示索引位置，之后在数据集中选取列数data[np.where()[0],:]=...

（四）结果测试

data_X = loadDataSet("testSet2.txt")

centroids,clusterAssment = binkMeans(data_X,)

plt.figure()

plt.scatter(data_X[:,].flatten(),data_X[:,].flatten(),c="b",marker="o")

print(centroids)

plt.scatter(centroids[:,].reshape(,).tolist()[],centroids[:,].reshape(,).tolist()[],c='r',marker="+")

plt.show()

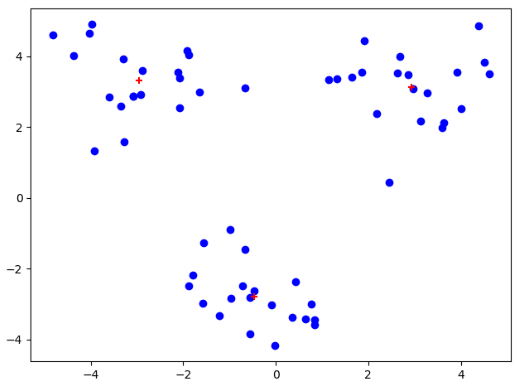
机器学习实战---K均值聚类算法的更多相关文章

  1. k均值聚类算法原理和（TensorFlow）实现

    顾名思义,k均值聚类是一种对数据进行聚类的技术,即将数据分割成指定数量的几个类,揭示数据的内在性质及规律. 我们知道,在机器学习中,有三种不同的学习模式:监督学习.无监督学习和强化学习: 监督学习,也 ...

  2. 机器学习之K均值聚类

      聚类的核心概念是相似度或距离,有很多相似度或距离的方法,比如欧式距离.马氏距离.相关系数.余弦定理.层次聚类和K均值聚类等 1. K均值聚类思想   K均值聚类的基本思想是,通过迭代的方法寻找K个 ...

  3. 100天搞定机器学习|day44 k均值聚类数学推导与python实现

    [如何正确使用「K均值聚类」? 1.k均值聚类模型 给定样本,每个样本都是m为特征向量,模型目标是将n个样本分到k个不停的类或簇中,每个样本到其所属类的中心的距离最小,每个样本只能属于一个类.用C表示 ...

  4. K均值聚类算法

    k均值聚类算法(k-means clustering algorithm)是一种迭代求解的聚类分析算法,其步骤是随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个 ...

  5. 基于改进人工蜂群算法的K均值聚类算法（附MATLAB版源代码）

    其实一直以来也没有准备在园子里发这样的文章,相对来说,算法改进放在园子里还是会稍稍显得格格不入.但是最近邮箱收到的几封邮件让我觉得有必要通过我的博客把过去做过的东西分享出去更给更多需要的人.从论文刊登 ...

  6. K均值聚类算法的MATLAB实现

    1.K-均值聚类法的概述    之前在参加数学建模的过程中用到过这种聚类方法,但是当时只是简单知道了在matlab中如何调用工具箱进行聚类,并不是特别清楚它的原理.最近因为在学模式识别,又重新接触了这 ...

  7. 机器学习实战5：k-means聚类：二分k均值聚类+地理位置聚簇实例

    k-均值聚类是非监督学习的一种,输入必须指定聚簇中心个数k.k均值是基于相似度的聚类,为没有标签的一簇实例分为一类. 一 经典的k-均值聚类 思路: 1 随机创建k个质心(k必须指定,二维的很容易确定 ...

  8. 机器学习理论与实战（十）K均值聚类和二分K均值聚类

    接下来就要说下无监督机器学习方法,所谓无监督机器学习前面也说过,就是没有标签的情况,对样本数据进行聚类分析.关联性分析等.主要包括K均值聚类(K-means clustering)和关联分析,这两大类 ...

  9. 聚类之K均值聚类和EM算法

    这篇博客整理K均值聚类的内容,包括: 1.K均值聚类的原理: 2.初始类中心的选择和类别数K的确定: 3.K均值聚类和EM算法.高斯混合模型的关系. 一.K均值聚类的原理 K均值聚类(K-means) ...

随机推荐

  1. cb50a_c++_STL_算法_局部排序partial_sort

    cb50a_c++_STL_算法_局部排序partial_sort partial_sort(b,se,e)排序一部分,begin,source end,endcout << " ...

  2. 定量度量程序复杂度的McCabe方法

    [本文版权归微信公众号"代码艺术"(ID:onblog)所有,若是转载请务必保留本段原创声明,违者必究.若是文章有不足之处,欢迎关注微信公众号私信与我进行交流!] 请画出下面代码的 ...

  3. springcloud2.0 添加配置中心遇到的坑

    新手入门,在springcloud 配置config的时候遇到了几个比较烦的坑 先说1.5x版本的一些配置吧 首先是端点暴露的方式 management: security: enabled: fal ...

  4. 实战：IDEA运行速度调优

    序言 可能大家觉得系统调优一般都是针对服务端应用而言的,普通Java开发人员很少有机会实践.今天就通用一个Java开发人员日常工作中经常使用的开发工具开做一次调优实战. 我在日常工作中的主要IDE工具 ...

  5. HDU3686 Traffic Real Time Query【缩点+lca】

    题目 City C is really a nightmare of all drivers for its traffic jams. To solve the traffic problem, t ...

  6. 一个ACE 架构的 C++ Timer

    .h #ifndef _Timer_Task_ #define _Timer_Task_ #pragma once #include <ace/Task.h> #include <a ...

  7. CSRF 跨站请求伪造学习笔记

    参考文章: 漏洞挖掘之CSRF CSRF花式绕过Referer技巧 What-是什么 CSRF(Cross-site request forgery)跨站请求伪造.攻击者通过构造特殊链接或者页面,盗用 ...

  8. https http 混合访问_https 页面中引入 http 资源的解决方式

    解决android 5.0 webview不能加载http与https混合内容的问题 在使用WebView加载https资源文件时,如果认证证书不被Android认可,那么会出现无法成功加载对应资源问 ...

  9. 什么是X-UA-Compatible？X-UA-Compatible的作用

    代码 <meta http-eqiv="X-UA-Compatible" content="ie=edge"> 什么是X-UA-Compatible ...

  10. 【git】配置git命令行别名

    引言:由于有些git命令较长,记起来比较麻烦,为了git工具使用的方便,为命令行取别名有很大的必要. 1.在家目录添加.gitconfig文件. 此文件在创建git仓库时,一般是没有的,需要手动添加. ...