GAMES101系列笔记一 图形学概述与线性代数入门

概述+线性代数

为什么学习图形学？

Computer Graphics is AWESOME!

主要涉及内容：

• 光栅化
• 曲线和网格
• 光线追踪
• 动画与模拟

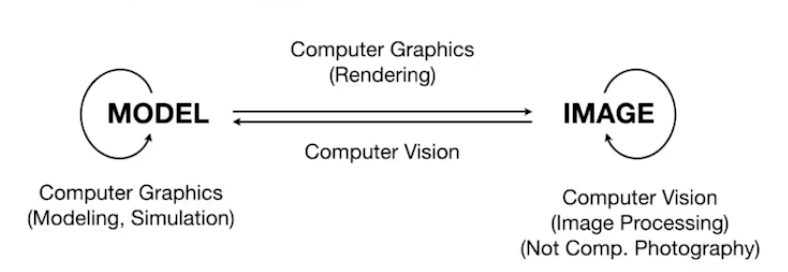
Differences between CG and CV:

线性代数回顾

向量（Vectors）

• 方向和长度

  模长：\(||\vec{a}||\)

• 没有确定的起点

• 单位向量：模长为1

  单位化向量： \(\hat{a} = \vec{a}/||\vec{a}||\)

• 向量求和：

  

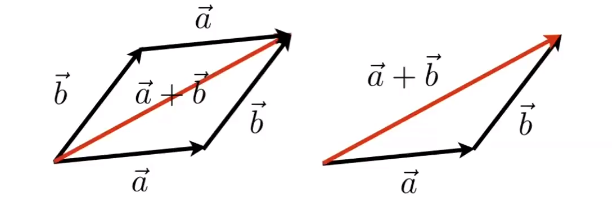
• 列向量，转置，模长的计算方式

  \(\boldsymbol{A} = \begin{pmatrix}x \\ y\end{pmatrix} \quad \boldsymbol{A}^T = \begin{pmatrix}x&y\end{pmatrix} \quad ||\boldsymbol{A}|| = \sqrt{x^2+y^2}\)

• 点乘（Dot/scalar Product）

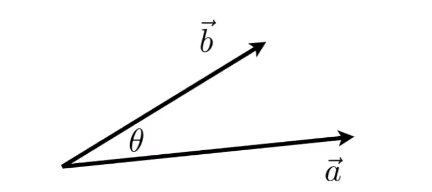
• 点乘定义：

  \(\vec{a} \cdot \vec{b} = ||\vec{a}||\,||\vec{b}||cos\theta\)

  \(cos\theta = \frac{\vec{a}\cdot\vec{b}}{||\vec{a}\||\,||\vec{b}||}\)

• For unit vectors:

  \(cos\theta = \hat{a}\cdot\hat{b}\)

• 交换律、结合律、数乘

直角坐标系下,计算更为方便：

• 2D:

  \(\vec{a}\cdot\vec{b} = \begin{pmatrix}x_a \\y_a\end{pmatrix}\cdot\begin{pmatrix}x_b \\y_b\end{pmatrix} = x_ax_b+y_ay_b.\)

• 3D:

  \(\vec{a}\cdot\vec{b} = \begin{pmatrix}x_a \\y_a\\z_a\end{pmatrix}\cdot\begin{pmatrix}x_b \\y_b\\z_b\end{pmatrix} = x_ax_b+y_ay_b+z_az_b.\)

• 投影:

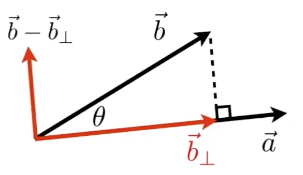
$\vec{b}_\perp:\vec{b}$ 在 $\vec{a}$ 上的投影;

$\vec{b}_\perp = k\hat{a};$ 

$k = ||\vec{b}_\perp|| = ||\vec{b}||cos\theta$

• 点乘可以告诉我们前和后的关系

• 叉乘（Cross\Vector product）

  • 两个向量相乘，得到一个与这两个向量都相等的向量；

    \(\vec{a}\times\vec{b} = -\vec{b}\times\vec{a}\)

    \(\vec{a}\times\vec{a} = \vec{0}\)

    \(||\vec{a}\times\vec{b}|| = ||\vec{a}||\,||\vec{b}||sin\phi\)

    方向由右手螺旋定则确定

    

  • 笛卡尔坐标系下的计算方法：

    \(\vec{a}\times\vec{b} = \begin{pmatrix}y_az_b-y_bz_a \\ z_ax_b - x_az_b \\ x_ay_b-y_ax_b\end{pmatrix} = A*b = \begin{pmatrix}0 & -z_a& y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0\end{pmatrix}\)

    \(A\) 为 \(\vec{a}\) 的对偶矩阵。

  • 叉乘在图形学中的作用

    判定左和右（一次叉乘），判断内和外（三次叉乘）

    

• 正交系

  • 三个单位向量

    $ ||\vec{u}|| = ||\vec{v}|| = ||\vec{w}|| = 1$

  • 两两垂直

  \(\vec{u}\cdot\vec{v} = \vec{v}\cdot\vec{w} = \vec{u}\cdot\vec{w}\)

  • 右手系

    \(\vec{w} = \vec{u}\times\vec{v}\)

  • 任何一个向量可以由这三个向量表示

    \(\vec{p} = (\vec{p}\cdot\vec{u})\vec{u} + (\vec{p}\cdot\vec{v})\vec{v} + (\vec{p}\cdot\vec{w})\vec{w}\)

    因为\(\vec{u}\ \vec{v}\ \vec{w}\) 都是单位向量，所以可以用 \(\vec{p}\) 在其上的投影乘以其本身来得到一个维度的分量。

• 矩阵（Matrices）

  • 矩阵乘矩阵

    维度需满足：

    \((M\times N)(N\times P) = (M\times P)\)

    （3 2）（2 4）= （3 4）

  

  • 不符合交换律。但符合结合律和分配律。

    \((AB)C = A(BC)\)

    \(A(B+C) = AB + AC\)

    \((A+B)C = AC + BC\)

  • 矩阵向量乘

    按 \(y\) 轴镜像

    \(\begin{pmatrix}-1 & 0 \\ 0 & 1\end{pmatrix}\begin{pmatrix}x \\ y \end{pmatrix} = \begin{pmatrix}-x \\ y\end{pmatrix}\)

  • 矩阵的转置

    \((AB)^T = B^TA^T\)

  • 单位矩阵

    \(I_{3\times3} = \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1\end{pmatrix}\)

    \(AA^{-1} = A^{-1}A = I;\quad (AB)^{-1} = B^{-1}A^{-1}\)

  • 向量乘法的矩阵形式

    \(\vec{a}\cdot\vec{b} = \vec{a}^T\vec{b}\)

    \(\vec{a}\times\vec{b} = \begin{pmatrix}y_az_b-y_bz_a \\ z_ax_b - x_az_b \\ x_ay_b-y_ax_b\end{pmatrix} = A^*b = \begin{pmatrix}0 & -z_a& y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0\end{pmatrix}\)