python的deque（双向）队列详解

首先 python的队列有很多种

Python标准库中包含了四种队列，分别是queue.Queue / asyncio.Queue / multiprocessing.Queue / collections.deque

可见deque是标准库collections中的

这其中最好用的是deque

以下是deque的基本操作：

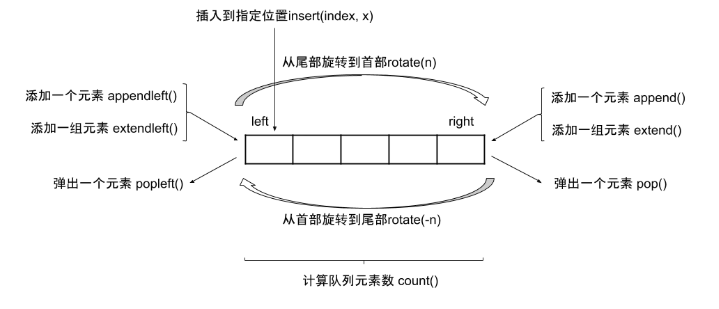
它的操作很像list 同时

相比于list实现的队列，deque实现拥有更低的时间和空间复杂度。list实现在出队（pop）和插入（insert）时的空间复杂度大约为O(n)，deque在出队（pop）和入队（append）时的时间复杂度是O(1)。

所以deque更有优越性 而且deque既可以表示队列 又可以表示栈 实在是太方便了

下面再介绍几个黑科技：

 

deque支持in操作符（真没想到这都支持）

1 q = collections.deque([1, 2, 3, 4])
2 print(5 in q)  # False
3 print(1 in q)  # True

还可以顺逆时针旋转...

# 顺时针
q = collections.deque([1, 2, 3, 4])
q.rotate(1)
print(q)  # [4, 1, 2, 3]
q.rotate(1)
print(q)  # [3, 4, 1, 2]

# 逆时针
q = collections.deque([1, 2, 3, 4])
q.rotate(-1)
print(q)  # [2, 3, 4, 1]
q.rotate(-1)
print(q)  # [3, 4, 1, 2]

还可以复制一个新队列：

>>> d.append(1)
>>> d.append(2)
>>> d
deque([1, 2])
>>> d1 = d.copy()
>>> d1
deque([1, 2])

 值得注意的是 deque里边的形式是列表形式

所以 试试extend呢？

>>> d.clear()
>>> d.append(1)
>>> d.extend([3,4,5])
>>> d
deque([1, 3, 4, 5])

能不能从左边extend呢：

>>> d.clear()
>>> d.append(1)
>>> d.extendleft([3,4,5])
>>> d
deque([5, 4, 3, 1])

还有index：查找索引位置

>>> d.extend(["a","b","c","d","e","f"])
>>> d
deque(['a', 'b', 'c', 'd', 'e','f'])
>>> d.index("c",0,4) #指定查找的区间
2
>>> d.index("c",0,2)
error...

其他的一些基本操作 还有

d.insert（位置，元素）  在指定位置插入元素

d.remove(元素）   删除指定元素

d.reverse   队列翻转

接下来我们做一道面试题：

题目

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

输入:
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]

既然时间复杂度是O（1）

我们用deque就好

代码：

from collections import deque
class MaxQueue:

    def __init__(self):
        self.d = deque()

    def max_value(self) -> int:
        return max(self.d) if self.d else -1

    def push_back(self, value: int) -> None:
        self.d.append(value)

    def pop_front(self) -> int:
        return self.d.popleft() if self.d else -1