dp2--合并石子（一）

dp2--合并石子（一）

一、心得

二、题目

石子合并（一）

时间限制：1000 ms  |  内存限制：65535 KB

难度：3

 

描述

    有N堆石子排成一排，每堆石子有一定的数量。现要将N堆石子并成为一堆。合并的过程只能每次将相邻的两堆石子堆成一堆，每次合并花费的代价为这两堆石子的和，经过N-1次合并后成为一堆。求出总的代价最小值。

 

输入

有多组测试数据，输入到文件结束。
每组测试数据第一行有一个整数n，表示有n堆石子。
接下来的一行有n（0< n <200）个数，分别表示这n堆石子的数目，用空格隔开

输出

输出总代价的最小值，占单独的一行

样例输入

3
1 2 3
7
13 7 8 16 21 4 18

样例输出

9
239

来源

经典问题

三、分析

* 合并石子.cpp
* 分析：
* 状态：
* f[i][j]表示把第i堆石子到第j堆石子合并成一堆的最小代价
* sum[j]表示第1堆石子到第j堆石子的和
* 最终状态：
* f[1][n]
* 初始状态：
* f[i][i]=0;
* 状态转移方程：
* 假设最后一次合并是将（i，k）和（k+1,j）合并
* f[i][j]=min(f[i][k]+f[k+1][j]+sum[j]-sum[i-1]) (k>=i&&k<=j)

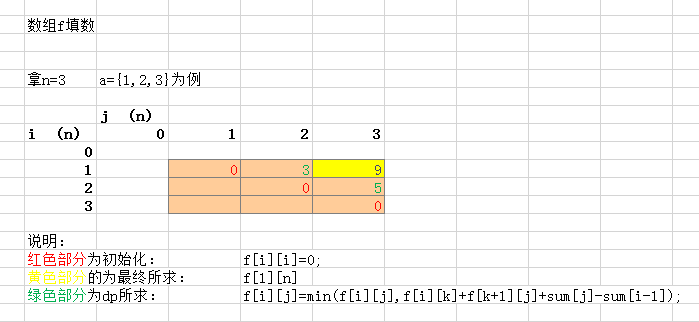
dp过程图

四、AC代码

242ms

 /*
  * 合并石子.cpp
  * 分析：
  * 状态：
  *         f[i][j]表示把第i堆石子到第j堆石子合并成一堆的最小代价
  *         sum[j]表示第1堆石子到第j堆石子的和
  * 最终状态：
  *         f[1][n]
  * 初始状态：
  *         f[i][i]=0;
  * 状态转移方程：
  *         假设最后一次合并是将（i，k）和（k+1,j）合并
  *        f[i][j]=min(f[i][k]+f[k+1][j]+sum[j]-sum[i-1]) (k>=i&&k<=j)
  *
  *
  */

 #include <iostream>
 #include <cstdio>
 using namespace std;
 int f[][];
 int sum[];
 int a[]; //用来存这n堆石子
 int n;

 void readData() {
     for (int i = ; i <= n; i++) {
         cin >> a[i];
     }
 }

 void printRead() {
     cout << "n:" << n << endl;
     for (int i = ; i <= n; i++) {
         cout << a[i] << " ";
     }
     cout << endl;
 }

 void initArr_sum() {
     sum[] = ;
     for (int i = ; i <= n; i++) {
         sum[i] = a[i] + sum[i - ];
     }
 }

 void printArr_sum() {
     for (int i = ; i <= n; i++) {
         cout << sum[i] << " ";
     }
     cout << endl;
 }

 void initArr_f() {
     //把上一轮的数据清空
     for (int i = ; i <= n; i++) {
         for (int j = ; j <= n; j++) {
             f[i][j] = 0xfffffff;
         }
     }
     //初始化
     for (int i = ; i <= n; i++) {
         f[i][i] = ;
     }
 }

 void printArr_f() {
     for (int i = ; i <= n; i++) {
         for (int j = ; j <= n; j++) {
             cout << f[i][j] << " ";
         }
         cout << endl;
     }
 }

 void init() {
     readData();
     //printRead();
     initArr_sum();
     //printArr_sum();
     initArr_f();
     //printArr_f();
 }

 void dp() {
     for (int i = n; i >= ; i--) {
         for (int j = i + ; j <= n; j++) {
             for (int k = i; k <= j; k++) {
                 f[i][j] = min(f[i][j],
                         f[i][k] + f[k + ][j] + sum[j] - sum[i - ]);
             }
         }
     }
 }

 void printAns() {
     cout << f[][n] << endl;
 }

 int main() {
     //freopen("src/in737.txt", "r", stdin);
     while (scanf("%d", &n)==) {
         init();
         dp();
         //printArr_f();
         printAns();
     }

     return ;
 }

 /*
  * 注意点：
  * 1、因为求最小值，所以f要初始化为较大值
  *         f[i][j] = 0xfffffff;
  */

五、注意点

1、因为求最小值，所以f要初始化为较大值
    f[i][j] = 0xfffffff;