uoj #297. 【CTSC2017】密钥

#297. 【CTSC2017】密钥

一个密钥是一个长度为 n=2k+1n=2k+1 的字符串，它包含 11 个字母X、kk 个字母 A 和 kk 个字母 B。例如 k=3k=3 时，BAXABAB 就是一个密钥。

如下图所示，可以按顺时针顺序把这 2k+12k+1 个字母排成一个圈：

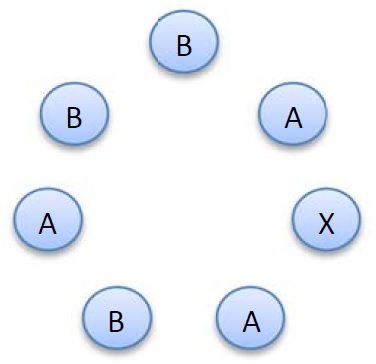
在 kk 个字母 A 中，有一部分可以定义为"强的"。

具体来说，从 X 出发顺时针走到某个 A 时，如果途中 A 的数目严格多于 B 的数目，则称此字母 A 为强的。

对于上面的例子来说，顺时针方向从字母 X 数起第 11 个和第 22 个字母 A 是强的，而第 33 个字母 A 不是强的。

一个密钥的特征值就是其中包含的强的字母 A 的个数。

天才小朋友 KT 给出了一个结论：

假设 kk 个字母 A 所在的位置已经固定，但是剩下的 kk 个 B 和 11 个 X 的位置是未知的。 （注意，满足这样要求的密钥一共有 k+1k+1 个，因为字母 X 还剩下 k+1k+1 个可能的位置。）

可以证明：所有这k+1k+1个可能的密钥的特征值是各不相同的，它们恰好为0,1,2,…,k0,1,2,…,k。

下页的图是一个具体的示例，从左到右的四个子图中分别有3个，2个，1个，0个字母A是强的。

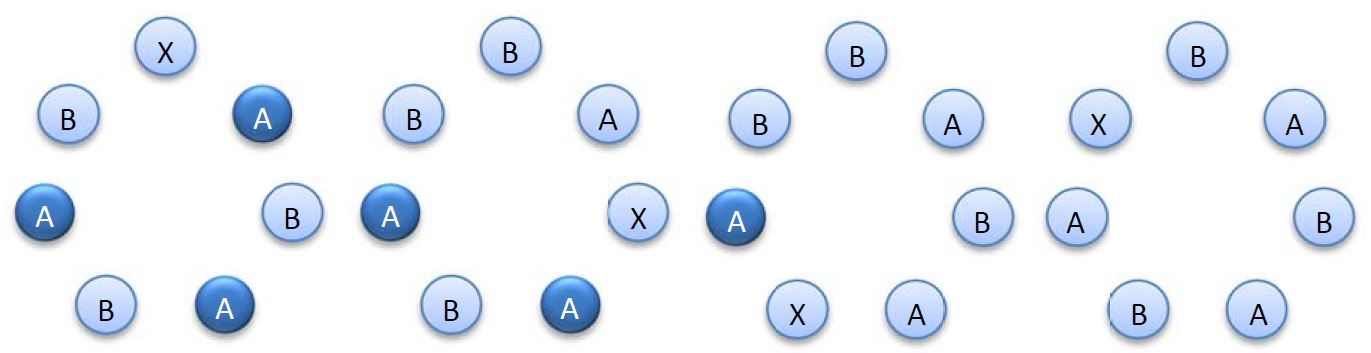
类似地，如果固定 kk 个字母 B 的位置，那满足条件的所有 k+1k+1 个密钥的特征值也各不相同，恰好为 0,1,⋯,k0,1,⋯,k。

现在你需要解决以下三个问题：

1. 给定密钥中所有 A 的位置，当密钥的特征值为 00 时，请问 X 在哪个位置。
2. 给定密钥中所有 A 的位置，当密钥的特征值为 SS 时，请问 X 在哪个位置。
3. 给定密钥中所有 B 的位置，当密钥的特征值为 SS 时，请问 X 在哪个位置。

注意：字符串的 2k+12k+1 个字母的位置由 11 到 2k+12k+1 编号。

例子一

假定 k=3,S=2k=3,S=2。那么：

当 A 的位置是 {2,4,6}{2,4,6} 且特征值为 00 时，X 的位置在 77；

当 A 的位置是 {2,4,6}{2,4,6} 且特征值为 22 时，X 的位置在 33；

当 B 的位置是 {2,4,6}{2,4,6} 且特征值为 22 时，X 的位置在 55。

例子二

假定 k=9,S=7k=9,S=7。那么：

当 A 的位置是 {3,4,5,9,10,12,13,16,19}{3,4,5,9,10,12,13,16,19} 且特征值为 00 时，X 的位置在 1414；

当 A 的位置是 {3,4,5,9,10,12,13,16,19}{3,4,5,9,10,12,13,16,19} 且特征值为 77 时，X 的位置在 1818；

当 B 的位置是 {3,4,5,9,10,12,13,16,19}{3,4,5,9,10,12,13,16,19} 且特征值为 77 时，X 的位置在 1717。

输入格式

只包含一组测试数据。

第一行包含一个整数kk，意义如题所述。

第二行包含一个整数seedseed，这个数将用于生成一个kk元集合P。

第三行包含一个整数SS，意义如题所述。

保证0≤S≤k≤1070≤S≤k≤107。1≤seed≤100001≤seed≤10000。

在下发文件中，包含三个用于生成输入数据的文件cipher.cpp/c/pas。其中读入部分已经完成，在数组 p[]p[] 中，若 p[i]=0p[i]=0，表示 ii 不属于集合PP，否则，ii 属于集合 PP。

输出格式

输出三行，每行一个数，依次对应问题描述中的三个子问题的答案。

即：

1. 第一个数表示当 kk 元集合 PP 代表 A 的位置且特征值为 00 时 X 的位置。
2. 第二个数表示当 kk 元集合 PP 代表 A 的位置且特征值为 SS 时 X 的位置。
3. 第三个数表示当 kk 元集合 PP 代表 B 的位置且特征值为 SS 时 X 的位置。

样例一

input

5
3344
2

output

10
1
2

explanation

第一个样例中，PP 数组为 11 的元素的下标分别为 5,6,7,8,95,6,7,8,9。

样例二

input

500000
4545
234567

output

999992
246922
753067

限制与约定

对于 30%30% 的数据，k≤103k≤103。

对于 50%50% 的数据，k≤105k≤105。

对于 100%100% 的数据，k≤107k≤107。

对于每个测试点,得分为以下三部分得分之和：

1. 如果第一问回答正确，你将获得 33 分。
2. 如果第二问回答正确，你将获得 44 分。
3. 如果第三问回答正确，你将获得 33 分。

如果你仅仅知道部分答案，请也务必按此格式要求输出三个数。否则你可能会因格式错误无法得分。

时间限制：1s1s

空间限制：512MB

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 20000005
using namespace std;
int p[maxn],b[maxn],cnt,ans[maxn];
int seed, n, k, S;
int getrand()
{
    seed = ((seed * ) ^ ) % ;
    return seed;
}
void generateData()
{
    scanf("%d%d%d",&k,&seed,&S);
    int t = ;
    n = k *  + ;
    memset(p, , sizeof(p));
    for (int i = ; i <= n; i++)
    {
        p[i] = (getrand() / ) % ;
        t += p[i];
    }
    int i = ;
    while (t > k)
    {
        while (p[i] == )
            i++;
        p[i] = ;
        t--;
    }
    while (t < k)
    {
        while (p[i] == )
            i++;
        p[i] = ;
        t++;
    }
}
int count1(int s){
    int sa=,sb=,res=;
    for(int i=,j=s+;i<=n;i++,j++){
        if(p[j]==)sb++;
        else {
            sa++;
            if(sa>sb)res++;
        }
    }
    return res;
}
void work1(){
    for(int i=;i<=cnt;i++)//x的位置
        ans[i]=count1(b[i]);
}
int count2(int s){
    int sa=,sb=,res=;
    for(int i=,j=s+;i<=n;i++,j++){
        if(p[j]==)sb++;
        else {
            sa++;
            if(sa>sb)res++;
        }
    }
    return res;
}
void work2(){
    for(int i=;i<=cnt;i++)
        ans[i]=count2(b[i]);
}
int main(){
    generateData();
    for(int i=;i<=n;i++)p[i-]=p[i];
    for(int i=;i<n;i++)p[i+n]=p[i];
    for(int i=;i<n;i++)if(!p[i])b[++cnt]=i;
    if(k<=){
        work1();
        int ans0,ans1;
        for(int i=;i<=cnt;i++){
            if(ans[i]==)ans0=b[i]+;
            if(ans[i]==S)ans1=b[i]+;
        }
        printf("%d\n%d\n",ans0,ans1);
        work2();
        for(int i=;i<=cnt;i++)
            if(ans[i]==S){
                printf("%d\n",b[i]+);
                return ;
            }
    }
    return ;
}

30分 暴力