HDU-1052（贪心策略）

Tian Ji -- The Horse Racing

Problem Description

Here is a famous story in Chinese history.

"That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others."

"Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser."

"Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian's. As a result, each time the king takes six hundred silver dollars from Tian."

"Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match."

"It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king's regular, and his super beat the king's plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?"

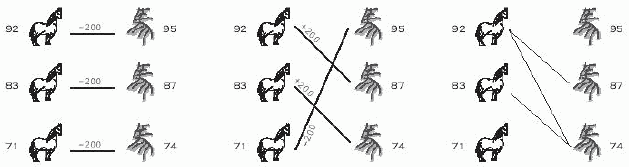
Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian's horses on one side, and the king's horses on the other. Whenever one of Tian's horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching...

However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses --- a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.

In this problem, you are asked to write a program to solve this special case of matching problem.

 

Input

The input consists of up to 50 test cases. Each case starts with a positive integer n (n <= 1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian’s horses. Then the next n integers on the third line are the speeds of the king’s horses. The input ends with a line that has a single 0 after the last test case.

 

Output

For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.

 

Sample Input

3

92 83 71

95 87 74

2

20 20

20 20

2

20 19

22 18

0

 

Sample Output

200

0

0

分析：题意就是田忌赛马的扩展，田忌和国王每个人有n匹马，然后两个人每匹马两两对应匹配，谁的马速度快谁就赢一局，求怎么匹配使得田忌赢的局数尽可能多。

题目有个误解让人以为是二分图最大匹配，其实是个贪心，但对我来说不好想。分三种情况：

1.田忌最慢的马比国王最慢的马还慢，则拿去与国王最快的马PK，反正都是输，不如拿去把对方最快的比掉，则后面马赢的机会就更大。

　　　2.田忌最慢的马比国王最慢的马快，则田忌赢一局。

　　  3.田忌最慢的马与国王最慢的马速度相等，则不能打平，因为打平与一平一负效果等价，还不如把田忌最慢的马去与国王最快的马比，为后面的马争取更大的赢的机会。

 #include <cstdio>
 #include <cmath>
 #include <cstring>
 #include <ctime>
 #include <iostream>
 #include <algorithm>
 #include <set>
 #include <vector>
 #include <sstream>
 #include <queue>
 #include <typeinfo>
 #include <fstream>
 #include <map>
 #include <stack>
 using namespace std;
 #define INF 100000
 typedef long long ll;
 const int maxn=;
 int tian[maxn],king[maxn];
 int main()
 {
 //    freopen("in.txt","r",stdin);
 //    freopen("out.txt","w",stdout);
     int n;
     while(scanf("%d",&n)){
         if(n==) break;
         memset(tian,,sizeof(tian));
         memset(king,,sizeof(king));
         for(int i=;i<n;i++)
             scanf("%d",&tian[i]);
         for(int i=;i<n;i++)
             scanf("%d",&king[i]);
         sort(tian,tian+n);
         sort(king,king+n);
         int win=,lose=;
         int t_low=,t_best=n-,k_low=,k_best=n-;
         while(t_low<=t_best){
             if(tian[t_low]>king[k_low]){
                 win++;
                 t_low++;
                 k_low++;
             }
             else if(tian[t_low]<king[k_low]){
                 lose++;
                 t_low++;
                 k_best--;
             }
             else{
                 if(tian[t_best]>king[k_best]){
                     win++;
                     t_best--;
                     k_best--;
                 }
                 else{
                     if(tian[t_low]<king[k_best])
                         lose++;
                     t_low++;
                     k_best--;
                 }
             }
         }
         int ans=(win-lose)*;
         printf("%d\n",ans);
     }
     return ;
 }