振兴中华|2013年蓝桥杯A组题解析第三题-fishers

标题: 振兴中华

小明参加了学校的趣味运动会，其中的一个项目是：跳格子。

地上画着一些格子，每个格子里写一个字，如下所示：（也可参见p1.jpg）

从我做起振

我做起振兴

做起振兴中

起振兴中华

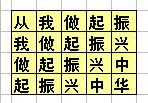
比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。

要求跳过的路线刚好构成“从我做起振兴中华”这句话。

请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

答案是一个整数，请通过浏览器直接提交该数字。

注意：不要提交解答过程，或其它辅助说明类的内容。

答案：35

代码一：递归，组合计数

可以从图中看出，往下走或者往右走都是满足要求的方案。

#include <iostream>

using namespace std;

int f(int x, int y) {
    if (x == 3 || y == 4)return 1;
    return f(x + 1, y) + f(x, y + 1);
}

int main(int argc, const char *argv[]) {
    cout << f(0, 0) << endl;
    return 0;
}

代码二：dfs搜索回溯

一开始没发现”图中往下走或者往右走都是满足要求的方案“，这个规律。

于是开始了dfs搜索。

类似于2D网格寻路，把”从我做起振兴中华，对应数:12345678“

#include<bits/stdc++.h>
using namespace std;

/*
dfs搜索路线
从我做起振兴中华 对应的数:12345678

12345
23456
34567
45678

*/
int a[4][5] = {1,2,3,4,5,2,3,4,5,6,3,4,5,6,7,4,5,6,7,8};
int vst[4][5];
int dr[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
int b[8] = {1,2,3,4,5,6,7,8};
int ans = 0;

bool in(int x,int y){
	return x>=0 && x<=3 && y>=0 && y<=4;
}

void dfs(int k,int x,int y){
	if(k == 7 && x == 3 && y == 4){
		ans++;
		return;
	}
	if(k>7)return;
	if(!in(x,y))return;
	vst[x][y] = 1;
	for(int i=0;i<4;i++){
		int tx = x + dr[i][0];
		int ty = y + dr[i][1];
		if(in(tx,ty) && !vst[tx][ty] && a[tx][ty] == b[k+1]){
			dfs(k+1,tx,ty);
		}
	}
	vst[x][y] = 0;
}

int main(){
	vst[0][0] = 1;
	dfs(0,0,0);
	cout<<ans<<endl;
	return 0;
}

//35

代码三：可以记忆化搜索（缓存）优化