时间序列异常检测算法S-H-ESD

1. 基于统计的异常检测

Grubbs' Test

Grubbs' Test为一种假设检验的方法，常被用来检验服从正太分布的单变量数据集（univariate data set）\(Y\) 中的单个异常值。若有异常值，则其必为数据集中的最大值或最小值。原假设与备择假设如下：

\(H_0\): 数据集中没有异常值
\(H_1\): 数据集中有一个异常值

Grubbs' Test检验假设的所用到的检验统计量（test statistic）为

\[
G = \frac{\max |Y_i - \overline{Y}|}{s}
\]

其中，\(\overline{Y}\)为均值，\(s\)为标准差。原假设\(H_0\)被拒绝，当检验统计量满足以下条件

\[
G > \frac{(N-1)}{\sqrt{N}}\sqrt{\frac{ (t_{\alpha/(2N), N-2})^2}{N-2 + (t_{\alpha/(2N), N-2})^2}}
\]

其中，\(N\)为数据集的样本数，\(t_{\alpha/(2N), N-2}\)为显著度(significance level)等于\(\alpha/(2N)\)、自由度（degrees of freedom）等于\(N-2\)的t分布临界值。实际上，Grubbs' Test可理解为检验最大值、最小值偏离均值的程度是否为异常。

ESD

在现实数据集中，异常值往往是多个而非单个。为了将Grubbs' Test扩展到\(k\)个异常值检测，则需要在数据集中逐步删除与均值偏离最大的值（为最大值或最小值），同步更新对应的t分布临界值，检验原假设是否成立。基于此，Rosner提出了Grubbs' Test的泛化版ESD（Extreme Studentized Deviate test）。算法流程如下：

• 计算与均值偏离最远的残差，注意计算均值时的数据序列应是删除上一轮最大残差样本数据后；

\begin{equation}
R_j = \frac{\max_i |Y_i - \overline{Y'}|}{s}, \quad 1 \leq j \leq k
\label{eq:esd_test}
\end{equation}

• 计算临界值（critical value）；

\[
\lambda_j = \frac{(n-j) * t_{p,n-j-1}}{\sqrt{(n-j-1+t_{p,n-j-1}^2)(n-j+1)}}, \quad 1 \leq j \leq k
\]

• 检验原假设，比较检验统计量与临界值；若\(R_i > \lambda_j\)，则原假设\(H_0\)不成立，该样本点为异常点；

• 重复以上步骤\(k\)次至算法结束。

2. 时间序列的异常检测

鉴于时间序列数据具有周期性（seasonal）、趋势性（trend），异常检测时不能作为孤立的样本点处理；故而Twitter的工程师提出了S- ESD (Seasonal ESD)与S-H-ESD (Seasonal Hybrid ESD)算法，将ESD扩展到时间序列数据。

S-ESD

STL将时间序列数据分解为趋势分量、周期分量和余项分量。想当然的解法——将ESD运用于STL分解后的余项分量中，即可得到时间序列上的异常点。但是，我们会发现在余项分量中存在着部分假异常点（spurious anomalies）。如下图所示：

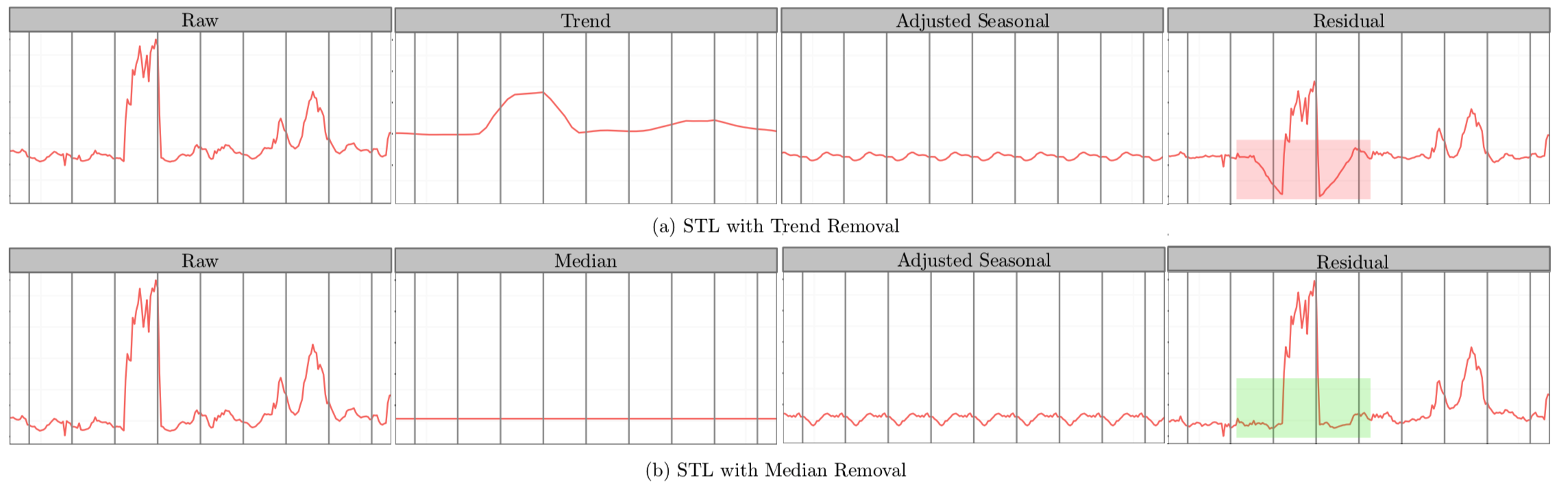
在红色矩形方框中，向下突起点被误报为异常点。为了解决这种假阳性降低准确率的问题，S-ESD算法用中位数（median）替换掉趋势分量；余项计算公式如下：

\[
R_X = X - S_X- \tilde{X}
\]

其中，\(X\)为原时间序列数据，\(S_X\)为STL分解后的周期分量，\(\tilde{X}\)为\(X\)的中位数。

S-H-ESD

由于个别异常值会极大地拉伸均值和方差，从而导致S-ESD未能很好地捕获到部分异常点，召回率偏低。为了解决这个问题，S-H-ESD采用了更具鲁棒性的中位数与绝对中位差（Median Absolute Deviation, MAD）替换公式\eqref{eq:esd_test}中的均值与标准差。MAD的计算公式如下：

\[
MAD = median(|X_i - median(X)|)
\]

S-H-ESD的Python实现有pyculiarity，时间序列异常检测数据集有Yahoo公开的A Labeled Anomaly Detection Dataset。

3. 参考资料

[1] Hochenbaum, Jordan, Owen S. Vallis, and Arun Kejariwal. "Automatic Anomaly Detection in the Cloud Via Statistical Learning." arXiv preprint arXiv:1704.07706 (2017).