【数据结构与算法】二叉树的 Morris 遍历（前序、中序、后序）

前置说明

不了解二叉树非递归遍历的可以看我之前的文章【数据结构与算法】二叉树模板及例题

Morris 遍历

概述

Morris 遍历是一种遍历二叉树的方式，并且时间复杂度O(N)，额外空间复杂度O(1) 。通过利用原树中大量空闲指针的方式，达到节省空间的目的

分析

设一棵二叉树有 n 个节点，则所有节点的指针域总和为 2 * n ，所有节点的非空指针域总和为 n - 1（非根节点被一个指针指向，根节点不被指针指向），所有节点的空指针域总和为 2n - (n - 1) = n + 1。

可以看到有大量的空指针域没有用到，在可以改变原二叉树结构的前提下，我们可以通过合理利用节点的空指针域，不开辟额外空间进行二叉树的非递归遍历。

那么先序、中序、后序遍历的节点访问顺序是如何确定的呢

如上图，根据紫色箭头顺序访问，第一次访问到的节点组成的集合就是先序遍历的结果。类似的，第二次访问到的节点组成的集合就是中序遍历的结果；第三次访问到的节点组成的集合就是后序遍历的结果。

通过设置节点访问不同次数的操作就可以实现三种遍历。

Morris 遍历的实质：建立一种机制，对于没有左子树的节点只到达一次，对于有左子树的节点会到达两次

Morris 遍历的原则

假设来到当前节点 cur，开始时 cur 来到头节点位置

• 如果 cur 没有左孩子，cur向右移动(cur = cur.right)

• 如果 cur 有左孩子，找到左子树上最右的节点 mostRight

  • a.如果 mostRight 的右指针指向空，让其指向 cur， 然后 cur 向左移动(cur = cur.left)

  • b.如果 mostRight 的右指针指向 cur，让其指向 null， 然后 cur 向右移动(cur = cur.right)

• cur 为空时遍历停止

举个例子：

1️⃣ 首先 cur 来到头结点 1，按照 morris 原则的第二条第一点，它存在左孩子，cur 左子树上最右的节点为 5，它的 right 指针指向空，所以让其指向 1，cur 向左移动到2。

2️⃣ 2 有左孩子，且它左子树最右的节点 4 指向空，按照 morris 原则的第二条第一点,让 4 的 right 指针指向 2，cur 向左移动到 4

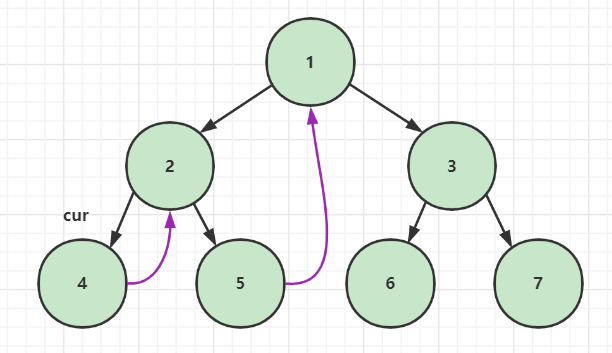
3️⃣ 4 不存在左孩子，按照 morris 原则的第一条，cur 向右移动，在第二步中，4 的 right 指针已经指向了 2，所以 cur 会回到 2

4️⃣ 重新回到 2，有左孩子，它左子树最右的节点为 4，但是在第二步中，4 的 right 指针已经指向了 2，不为空。所以按照 morris 原则的第二条第二点，cur 向右移动到 5，同时 4 的 right 指针重新指向空

5️⃣ 5 不存在左孩子，按照 morris 原则的第一条，cur 向右移动，在第一步中，5 的 right 指针已经指向了 1，所以 cur 会回到 1

6️⃣ cur 回到 1，回到头结点，左子树遍历完成，1 有左孩子，左子树上最右的节点为 5，它的 right 指针指向 1，按照 morris 原则的第二条第二点，1 向右移动到 3，同时 5 的 right 指针重新指回空

7️⃣ 3 有左孩子，且它左子树最右的节点 6 指向空，按照 morris 原则的第二条第一点,让 6 的 right 指针指向 3，cur 向左移动到 6

8️⃣ 6 不存在左孩子，按照 morris 原则的第一条，cur 向右移动，在第二步中，6 的 right 指针已经指向了 3，所以 cur 会回到 3

9️⃣ 重新回到 3，有左孩子，它左子树最右的节点为 6，但是在第二步中，6 的 right 指针已经指向了 3，不为空。所以按照 morris 原则的第二条第二点，cur 向右移动到 7，同时 6 的 right 指针重新指向空

1️⃣0️⃣ cur 没有左孩子，向右移动到 null，遍历停止

以上就是 Morris 遍历的全过程了，通过在遍历过程中适当的位置，即每个节点访问特定次数后设置操作，可以实现三种遍历

前序遍历

• 对于没有左子树的节点只到达一次，直接打印

• 对于有左子树的节点会到达两次，则在第一次到达时打印

public static void morrisPre(Node head) {
    if(head == null){
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null){
        // cur表示当前节点，mostRight表示cur的左孩子的最右节点
        mostRight = cur.left;
        if(mostRight != null){
            // cur有左孩子，找到cur左子树最右节点
            while (mostRight.right !=null && mostRight.right != cur){
                mostRight = mostRight.right;
            }
            // mostRight的右孩子指向空，让其指向cur，cur向左移动
            if(mostRight.right == null){
                mostRight.right = cur;
                System.out.print(cur.value+" ");  // 此时第一次访问节点
                cur = cur.left;
                continue;                         // 直接进入下一次循环
            }else {
                // mostRight的右孩子指向cur，让其指向空，cur向右移动
                mostRight.right = null;
            }
        }else {
            System.out.print(cur.value + " ");  // 没有左孩子的话直接输出，该节点就是第一次访问
        }
        cur = cur.right;
    }
    System.out.println();
}

中序遍历

• 对于没有左子树的节点只到达一次，直接打印

• 对于有左子树的节点会到达两次，第二次到达时打印

public static void morrisIn(Node head) {
    if(head == null){
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null){
        // cur表示当前节点，mostRight表示cur的左孩子的最右节点
        mostRight = cur.left;
        if(mostRight != null){
            // cur有左孩子，找到cur左子树最右节点
            while (mostRight.right !=null && mostRight.right != cur){
                mostRight = mostRight.right;
            }
            // mostRight的右孩子指向空，让其指向cur，cur向左移动
            if(mostRight.right == null){
                mostRight.right = cur;
                cur = cur.left;
                continue;                         // 直接进入下一次循环
            }else {                               // 第二次到达
                // mostRight的右孩子指向cur，让其指向空，cur向右移动
                mostRight.right = null;
            }
        }
        System.out.print(cur.value+" ");  // 没有左子树的节点只到达一次直接打印，对于有左子树的节点会到达两次，第二次到达时打印
        cur = cur.right;
    }
    System.out.println();
}

后序遍历

• 第二次访问节点时逆序打印该节点左树的右边界

• 最后单独打印整棵树的右边界

public static void morrisPos(Node head) {
       if(head == null){
           return;
       }
       Node cur = head;
       Node mostRight = null;
       while (cur != null){
           mostRight = cur.left;
           if(mostRight != null){
               while (mostRight.right !=null && mostRight.right != cur){
                   mostRight = mostRight.right;
               }
               if(mostRight.right == null){
                   mostRight.right = cur;
                   cur = cur.left;
                   continue;
               }else {
                   mostRight.right = null;
                   printEdge(cur.left);     // 第二次访问时逆序打印该节点左树的右边界
               }
           }
           cur = cur.right;
       }
       printEdge(head);     // 最后单独打印整棵树的右边界
       System.out.println();
   }
   public static void printEdge(Node node){   // 逆序打印：反转链表打印后再反转回原样
       Node tail =reverseEdge(node);
       Node cur = tail;
       while (cur != null ){
           System.out.print(cur.value+" ");
           cur =cur.right;
       }
       reverseEdge(tail);
   }
   public static Node reverseEdge(Node node){  // 链表反转
       Node pre = null;
       Node next = null;
       while (node != null){
           next = node.right;
           node.right = pre;
           pre = node;
           node = next;
       }
       return pre;
   }