Halum UVA - 11478 差分约束

输入输出格式

输入格式：

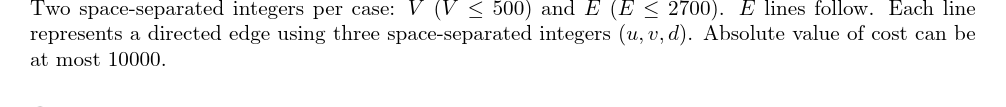
输出格式：

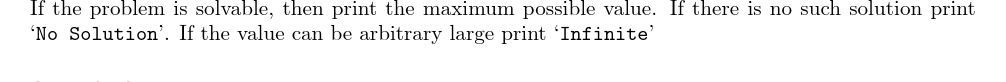
输入输出样例

输入样例#1： 复制

2 1
1 2 10
2 1
1 2 -10
3 3
1 2 4
2 3 2
3 1 5
4 5
2 3 4
4 2 5
3 4 2
3 1 0
1 2 -1

输出样例#1： 复制

Infinite
Infinite
3
1

最小值最大化-----> 二分答案转化为判定；
假设 i--->j 有一条权值为 wgt 的边，
那么我们操作后，假设此时我们要判定的答案为 mid;
∴ 应有 wgt + x[ i ]- x[ j ]>=mid;
其中 x[ i ] 表示在 i 点的操作值，
即： x[ j ]<=x[ i ]+ wgt - mid；
用差分约束解决；
判断是否有解判断是否存在环即可；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#pragma GCC optimize(2)
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 100005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)

inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/

ll qpow(ll a, ll b, ll c) {
	ll ans = 1;
	a = a % c;
	while (b) {
		if (b % 2)ans = ans * a%c;
		b /= 2; a = a * a%c;
	}
	return ans;
}

int n, m;
int fm[maxn], To[maxn], wgt[maxn];

struct node {
	int v, w;
	node(){}
	node(int v,int w):v(v),w(w){}

};

vector<node>vc[maxn];
int dis[maxn];
bool vis[maxn], inQueue[maxn];
int flag;

void spfa(int x) {
	if (flag)return;
	vis[x] = 1; inQueue[x] = 1;
	int Siz = vc[x].size();
	for (int i = 0; i < Siz; i++) {
		int v = vc[x][i].v;
		if (dis[v] > dis[x] + vc[x][i].w) {
			dis[v] = dis[x] + vc[x][i].w;
			if (!inQueue[v]) {
				spfa(v);
			}
			else {
				flag = 1; return;
			}
		}
	}
	inQueue[x] = 0;
}

bool check(int x) {
	flag = 0; ms(inQueue); ms(vis);
	memset(dis, 0x3f, sizeof(dis));
	for (int i = 1; i <= n; i++)vc[i].clear();
	for (int i = 1; i <= m; i++) {
		vc[fm[i]].push_back(node(To[i], wgt[i] - x));
	}
	for (int i = 1; i <= n; i++) {
		if (vis[i])continue;
		dis[i] = 0;
		spfa(i);
		if (flag)break;
	}
	if (flag)return false;
	else return true;
}

int main()
{
	//ios::sync_with_stdio(0);
	while (cin >> n >> m) {
		for (int i = 1; i <= m; i++) {
			rdint(fm[i]); rdint(To[i]); rdint(wgt[i]);
		}
		int l = 1, r = 1e5 + 1;
		int ans = 0;
		while (l <= r) {
			int mid = (l + r) / 2;
			if (check(mid))l = mid+1, ans = mid;
			else r = mid - 1;
		}
		if (ans <= 0)cout << "No Solution" << endl;
		else if (ans >= 50000)cout << "Infinite" << endl;
		else cout << ans << endl;
	}
    return 0;
}