[COGS 2583]南极科考旅行

2583. 南极科考旅行

★★   输入文件：BitonicTour.in   输出文件：BitonicTour.out   简单对比
时间限制：1 s   内存限制：256 MB

【题目描述】

小美要在南极进行科考，现在她要规划一下科考的路线。

地图上有 N 个地点，小美要从这 N 个地点中 x 坐标最小的地点 A，走到 x 坐标最大的地点 B，然后再走回地点 A。

请设计路线，使得小美可以考察所有的地点，并且在从 A 到 B 的路程中，考察的地点的 x 坐标总是上升的，在从 B 到 A 的过程中，考察的地点的 x 坐标总是下降的。

求小美所需要走的最短距离（欧几里得距离）。

【输入格式】

输入共 N+1 行。

第 1 行包含 1 个正整数 N，表示地图上共有 N 个地点。

第 1 +(1) 至 1 +(N) 行，每行包含 2 个正整数 x, y，表示其中 1 个地点的坐标。

【输出格式】

输出共 1 行。

第 1 行包含一个浮点数，表示小美需要走的最短距离，保留两位小数。

【样例输入】

4
1 1
2 3
4 1
3 2

【样例输出】

 8.06

【数据范围及约定】

对于前 20% 测试数据

3 <= N <= 6

1 <= x <= 20, 1 <= y <= 20

对于后 80% 测试数据

3 <= N <= 300

1 <= x <= 10000, 1 <= y <= 10000

对于全部测试点，保证每个点坐标的 x 值互不相同

【来源】

Bitonic Tour

题解

乍一看好像一脸 $DP$ 的样子...这种要走一个来回的情形似乎是之前的某个叫做小烈上菜的题...

然而居然出现在了网络流专题里...

行吧网络流就网络流...一开始感觉不会有费用流就开始构最大流(最小割)的图然而直接 $GG$ ...然后意识到是费用流...

woc我不会打费用流啊QAQ

$dbw$ 强行教学一波 $zkw$ 网络流...打完板子开始构图w

首先肯定是要按横坐标排序, 然后我们发现一去一回的方向并没有什么卵用, 找到一个环和找到两条路径是等价的. 这样我们可以发现, 每个结点都必须选择两条边, 其中 $x$ 最小的结点两条都是出边, 最大的结点两条都是入边, 其他结点一条入边一条出边, 这样的话我们可以得到这样的构图:

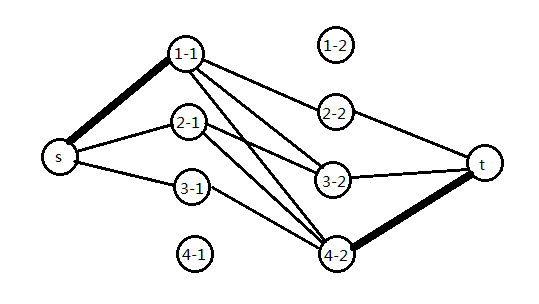
其中较粗的边容量为2, 较细的边容量为1, $s$ 连出的边和连向 $t$ 的边费用为 $0$ , 实际结点间边的距离即为欧几里得距离.

写 $zkw$ 网络流的话有一个坑点: 由于增广时要判断某条边是否在最短路上, 但是现在费用是一个实数, 所以会有精度问题, 直接使用  dis[s]+i->dis==dis[i->to]  判定的话会炸精度死循环, 这点需要注意OwO

参考代码

GitHub

 #include <bits/stdc++.h>
 
 const int MAXV=1e3+;
 const int MAXE=2e5+;
 const double INF=1e10;
 const int INFI=0x3F3F3F3F;
 const double EPSILON=1e-;
 
 struct Edge{
     int from;
     int to;
     int flow;
     double dis;
     Edge* rev;
     Edge* next;
 };
 Edge E[MAXE];
 Edge* head[MAXV];
 Edge* top=E;
 
 struct Node{
     double x;
     double y;
     bool friend operator<(const Node& a,const Node& b){
         return a.x<b.x;
     }
 };
 Node N[MAXV];
 
 int n;
 int v;
 bool vis[MAXV];
 double dis[MAXV];
 
 double Sqr(double);
 bool SPFA(int,int);
 int DFS(int,int,int);
 double Dinic(int,int);
 void Insert(int,int,double,int);
 double EucDis(const Node&,const Node&);
 
 int main(){
 #ifndef ASC_LOCAL
     freopen("BitonicTour.in","r",stdin);
     freopen("BitonicTour.out","w",stdout);
 #endif
     scanf("%d",&n);
     for(int i=;i<=n;i++){
         scanf("%lf%lf",&N[i].x,&N[i].y);
     }
     std::sort(N+,N++n);
     for(int i=;i<n;i++){
         Insert(,i<<,,);
         Insert(i<<|,,,);
     }
     Insert(,<<,,);
     Insert(n<<|,,,);
     v=n*+;
     for(int i=;i<=n;i++){
         for(int j=i+;j<=n;j++){
             Insert(i<<,j<<|,EucDis(N[i],N[j]),);
         }
     }
     printf("%.2f\n",Dinic(,));
     return ;
 }
 
 double Dinic(int s,int t){
     double ans=;
     while(SPFA(s,t)){
         memset(vis,,sizeof(vis));
         ans+=DFS(s,INFI,t)*dis[t];
     }
     return ans;
 }
 
 int DFS(int s,int flow,int t){
     if(s==t||flow==)
         return flow;
     int tmp=flow;
     int k;
     vis[s]=true;
     for(Edge* i=head[s];i!=NULL&&tmp>;i=i->next){
         if(i->flow>&&fabs(dis[i->from]+i->dis-dis[i->to])<EPSILON&&!vis[i->to]){
             k=DFS(i->to,std::min(tmp,i->flow),t);
             tmp-=k;
             i->flow-=k;
             i->rev->flow+=k;
         }
     }
     return flow-tmp;
 }
 
 bool SPFA(int s,int t){
     for(int i=;i<v;i++)
         dis[i]=INF;
     memset(vis,,sizeof(vis));
     std::queue<int> q;
     q.push(s);
     vis[s]=true;
     dis[s]=;
     while(!q.empty()){
         s=q.front();
         vis[s]=false;
         q.pop();
         for(Edge* i=head[s];i!=NULL;i=i->next){
             if(i->flow>&&dis[s]+i->dis<dis[i->to]){
                 dis[i->to]=dis[s]+i->dis;
                 if(!vis[i->to]){
                     q.push(i->to);
                     vis[i->to]=true;
                 }
             }
         }
     }
     return dis[t]<INFI;
 }
 
 void Insert(int from,int to,double dis,int flow){
     top->from=from;
     top->to=to;
     top->dis=dis;
     top->flow=flow;
     top->rev=top+;
     top->next=head[from];
     head[from]=top++;
 
     top->from=to;
     top->to=from;
     top->dis=-dis;
     top->flow=;
     top->rev=top-;
     top->next=head[to];
     head[to]=top++;
 }
 
 inline double EucDis(const Node& a,const Node& b){
     return sqrt(Sqr(a.x-b.x)+Sqr(a.y-b.y));
 }
 
 inline double Sqr(double x){
     return x*x;
 }

Backup