第八章——降维（Dimensionality Reduction）

机器学习问题可能包含成百上千的特征。特征数量过多，不仅使得训练很耗时，而且难以找到解决方案。这一问题被称为维数灾难（curse of dimensionality）。为简化问题，加速训练，就需要降维了。

降维会丢失一些信息（比如将图片压缩成jpeg格式会降低质量），所以尽管会提速，但可能使模型稍微变差。因此首先要使用原始数据进行训练。如果速度实在太慢，再考虑降维。

8.1 维数灾难（The Curse of Dimensionality）

我们生活在三维空间，连四维空间都无法直观理解，更别说更高维空间了（wiki有关四维空间的介绍，以及油管上的一个视频，将四维空间展开为三维空间）。高维空间和低维空间相比，还是用很大区别的。比如一个单位正方形，只有大概0.4%的部分是距离边界0.001以内的（这部分边缘的面积大概是$0.001 \times 1 \times 4 = 0.004$，占总体面积的0.4%）。但是在一个一万维的单位超立方体中，这一概率却变成了99.999999%，绝大多数点都在距离某一维度很近的地方。一个有趣的事实是，人类有许多不同的属性，你认识的所有人都可能是某一特征的极端分子（比如咖啡里的放糖量）。

还有一个更麻烦的区别：如果在单位正方形中任意选取两点，其距离平均大概是0.52（这道概率统计的习题，我已经不记得怎么求解了）。在单位立方体中这一距离是0.66。而在1000000维单位超立方体中，这一距离就增大到了408.25（大概$\sqrt{1000000/6}$）。这说明高维数据集很可能是相当稀疏的，样本实例间距离很大，预测是新的样本距离训练集样本的距离也很大，预测可信度远低于地位数据集。简单来说，高维数据集很容易过拟合。

理论上，维数灾难的一个解决方案是增加样本数量，从而使训练集达到足够的密度。可是这在实践中并不可行，因为其复杂度是指数级的。

8.2 主要降维方法（Main Approaches for Dimensionality Reduction）

8.2.1 投影（Projection）

如图8-2所示，可将三维数据集投影到合适的二维平面，

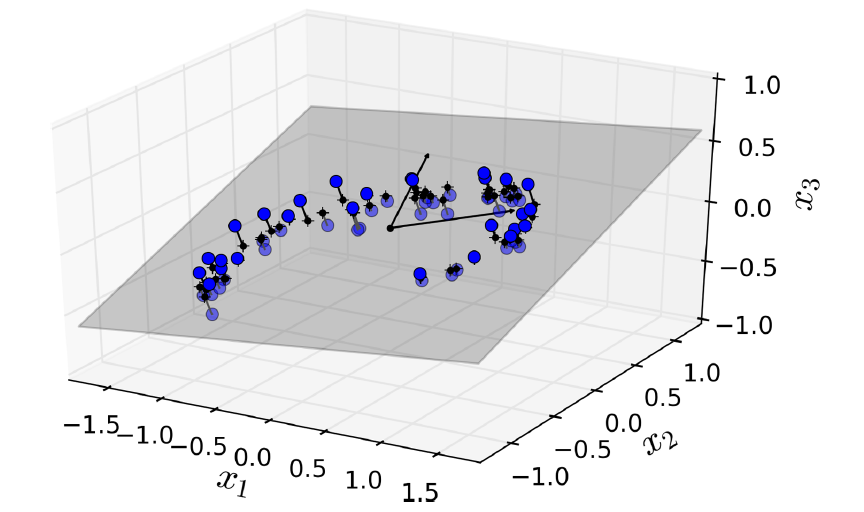
图8-2. 几乎位于同一平面的3D数据集

投影后的新数据集如图8-3所示。

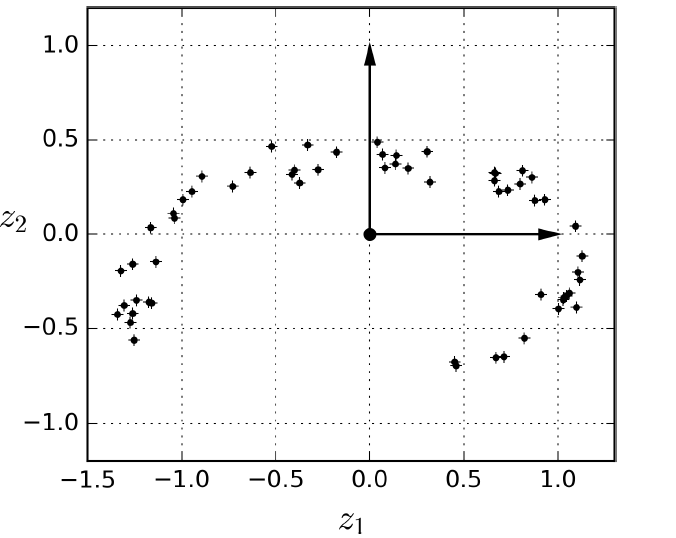
图8-3. 投影和的2D数据集

但有时候，投影是不好使的，例如图8-4所示的蛋糕卷数据集，尽管该数据集也是近似位于一个二维平面的（该数据集正确的降维方式是将蛋糕卷展开的二维平面）。

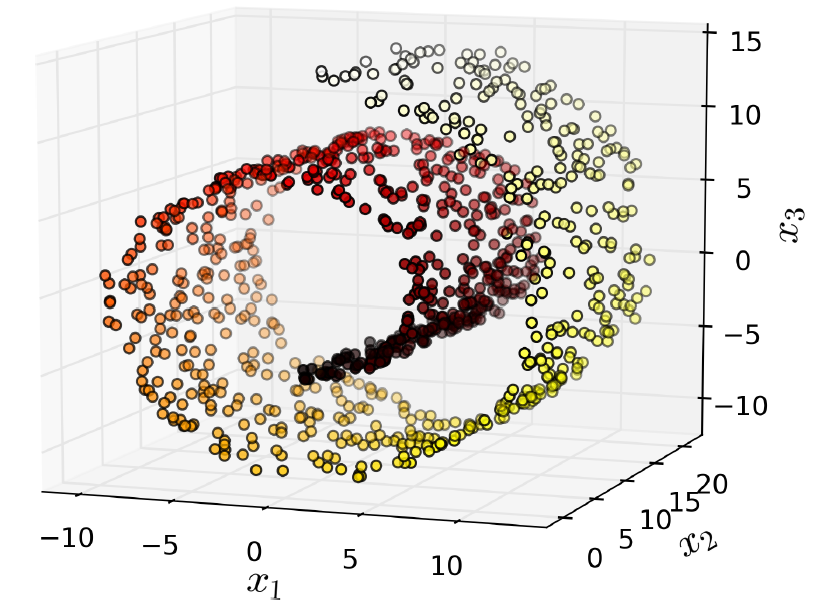
8-4. Swiss roll数据集

8.2.2 流形学习（Manifold Learning）

上面的蛋糕卷数据集就是一个2D流形。简单来讲，2D流形是一个在更高维空间中扭曲的2D形状。 当然，2D流形可以推广到n维流形。

许多降维算法就是对数据集所处于的流形建模，这被称作流行学习。

8.3 主成分分析（PCA）

主成分分析（Principal Component Analysis）是目前最受欢迎的降维算法。该算法首先找到距离数据集最近的低维超平面，然后就数据集投射到该超平面。

8.3.1 保留方差（Preserving the Variance）

将数据集投影到低维超平面之前，首先要选择合适的超平面。如图8-7所示，左侧是一个二维数据集，以及三个超平面（一维超平面）。右侧是数据集在相应超平面做投影后得到的新数据集。

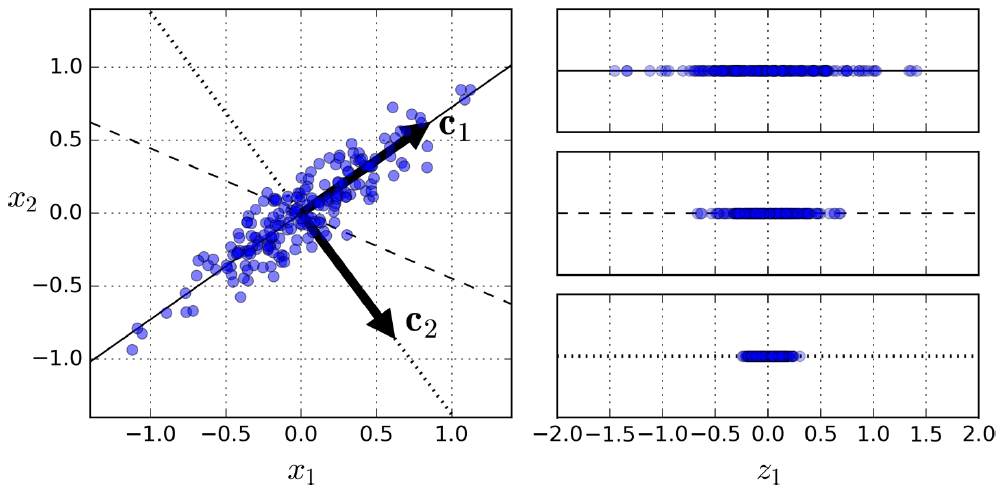
图8-7. 选择合适的子空间

很明显应该选择那条实心直线作为超平面，因为投影后新的数据集方差最大，损失的信息最少。此外，该超平面对应的新数据集，与原始数据集的欧氏距离最小。

8.3.2 主成分（Principal Components）

PCA可以识别出最大程度地保留训练数据集差异（variance）的坐标轴，也就是图8-7中的实线。然后找出第二个坐标轴，最大程度地保留剩下的差异，也就是图中与实线正交的虚线。用单位向量表示第$i$个坐标轴，这被称作第$i$个主成分。

可以使用奇异值分解（Singular Value Decomposition，SVD）得到主成分，$X = U \cdot \Sigma \cdot V^T$。

主成分矩阵：

\begin{align*}
V^T = \begin{pmatrix}
| &| & &| \\
c_1 &c_2 &\cdots &c_n \\
| &| & &|
\end{pmatrix}
\end{align*}

NumPy的svd() 函数可以进行奇异值分解：

X_centered = X - X.mean(axis=0)
U, s, V = np.linalg.svd(X_centered)

PCA假设数据集是以原点为中心的，只不过Scikit-Learn的PAC类会自动进行中心化。

8.3.3 投影到d维（Projecting Down to d Dimensions）

最佳超平面由前d个主成分向量组成，将训练集投影到该超平面即可，代码如下：

W2 = V.T[:, :2]
X2D = X_centered.dot(W2)

8.3.4 使用Scikit-Learn　　

from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X2D = pca.fit_transform(X)　

8.3.5 可解释方差比例（Explained Variance Ratio）

>>> print(pca.explained_variance_ratio_)
array([ 0.84248607, 0.14631839])

这说明第一个主成分承担了84.2%的差异，第二个主成分承担了14.6%的差异。

8.3.6 维数选择

与其武断地选择多杀维，不如选择足够保留大部分差异（比如95%）的维数。以下代码获取足以保留95%差异的代码：

pca = PCA()
pca.fit(X)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1　

然后设置n_components=d重新执行PCA：

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X)　

另一个选择是以维数为自变量，可释方差（explained variance）为因变量，画出函数图形：

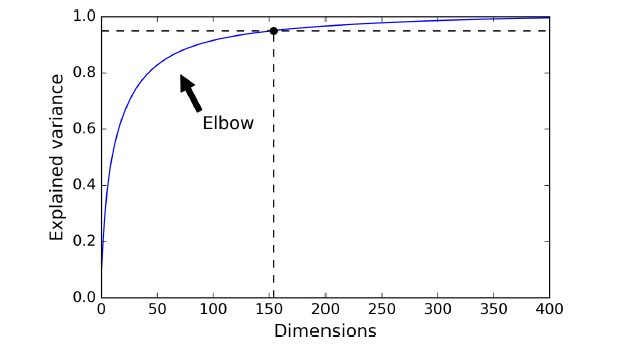
8.3.7 PCA用于压缩

在MNIST数据集应用PCA，保留95%的差异，仅需150个特征，远小于原始的784个特征，这是一个不错的压缩率。压缩之后还可以解压缩到784维，但这并不能得到原始数据，只是跟选择数据很接地，毕竟压缩做投影的时候丢失了一些信息。

8.3.8 Incremental PCA

感觉类似于最小批梯度下降

8.3.9 随机PCA（Randomized PCA）

可以加速运算

8.4 核PCA（Kernel PCA）

核PCA就是将核技巧应用于PCA，代码如下：

from sklearn.decomposition import KernelPCA
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)

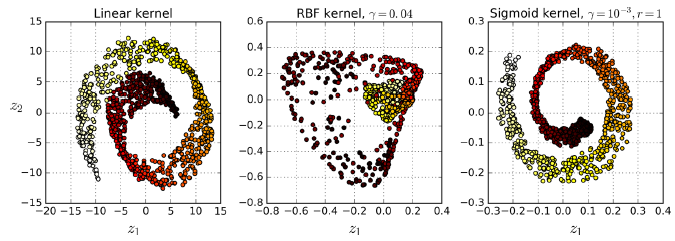
图8-10. 使用不同核将蛋糕卷数据集投影到2维

8.4.1 核的选择与超参数的调整（Selecting a Kernel and Tuning Hyperparameters）

这有两种情况。

第一种情况，尽管kPCA是无监督算法，没有明显的衡量指标帮助我们调整参数。减少降维的下一步往往是监督学习，比如分类。这就可以选择使得分类效果最好的参数。

第二种情况，完全是无监督学习，这是可以选择使得重构误差（reconstruction error）最小的超参数。

8.5 局部线性嵌入（Locally Linear Embedding，LLE）

LLE是另一种强大的非线性降维（nonlinear dimensionality reduction，NLDR）技术。该算法并不像PCA那样依赖投影，而是首先寻找每一个训练两本与其k个近邻（closest neighbors，c.n.）的线性关系，然后找到数据集的一种低维表示，其能够将这些近邻关系最好地保持。该算法对于卷曲数据集表现很好，尤其是噪声不多的情况下。

from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_reduced = lle.fit_transform(X)

　　

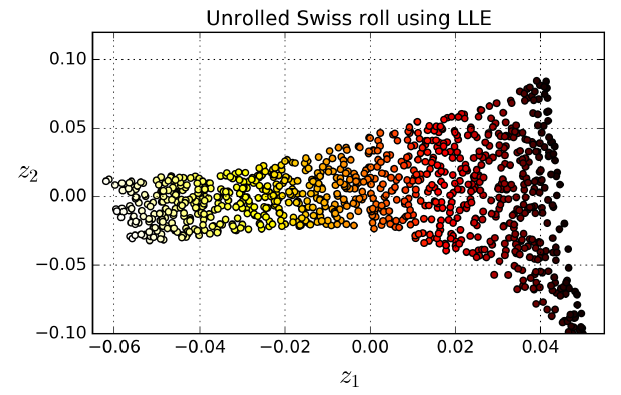
图8-12. 展开蛋糕卷数据集

如图8-12所示，蛋糕卷被展开了。然而，如果数据的范围过大，距离并不能良好的保持下来：蛋糕卷左侧被挤压，右侧被拉伸。

LLE工作方式如下：

首先，对于每一个训练样本$X^{(i)}$，识别出其$k$近邻，然后建立$X^{(i)}$与其$k$近邻的线性方程。

LLE第一步，局部线性关系模型：

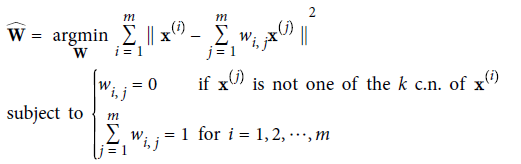
然后，将训练集映射（这里是映射，也就是map，不是前面的投影projecting）到d维空间（d<n），并尽可能地保持局部关系。

LLE第二步，降维并保留局部关系：

8.6 其它的降维技术（Other Dimensionality Reduction Techniques）

• Multidimensional Scaling (MDS)，保持样本距离降维。
• Isomap，在样本的近邻间创建图，降维时保持geodesic distances。
• t-Distributed Stochastic Neighbor Embedding (t-SNE)，降维时保持相似样本接近，不相似样本远离。这在样本可视化时很有用，尤其是样本簇的可视化。
• Linear Discriminant Analysis (LDA)，这实际上是一个分类算法，在训练的时候可以学习到最能区别类别的坐标轴，然后用这些坐标轴定义超平面并将样本映射于其上。其优势是可以尽可能地保持样本点分离，可以再应用分离算法（比如SVM）之前使用LDA。

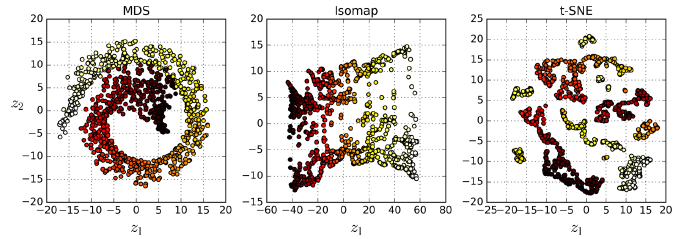
图8-13. 不同算法将蛋卷数据集映射到2维