Lightning Conductor 洛谷P3515 决策单调性优化DP

遇见的第一道决策单调性优化DP，虽然看了题解，但是新技能√，很开森。

先%FlashHu大佬，反正我是看了他的题解和精美的配图才明白的，%%%巨佬。

废话不多说，看题：

题目大意

已知一个长度为n的序列a1,a2,...,an。

对于每个1<=i<=n，找到最小的非负整数p满足 对于任意的j, aj < = ai + p - sqrt(abs(i-j))

数据范围

洛咕上也没给，我能怎么办啊

非正解做法一：暴力

应该都会吧，\(O(n^2)\)枚举。洛谷上貌似40pts。

非正解做法二：ST表优化

首先，我们将原式整理，可得\(p\geqslant a_j-a_i+\sqrt{\left | i-j \right |}\)，最终\(p_i\)即是\(max\{\left \lceil a_j-a_i+\sqrt{\left | i-j \right |} \right \rceil \}\)。

然后，我们发现，其实需要向上取整的只有\(\sqrt{\left | i-j \right |}\)这一部分，而它向上取整的值是连续分布的，即0,1,2,2,2,3,3,3,3,3,4......且如果知道i和j的值时，我们很容易知道同一个数开始的位置和结束的位置。

然后我们就可以用ST表来维护区间最大值，预计得分50pts。

（我没想到的）正解

经过观察式子，我们知道\(p_i\)的值取决于\(a_j+\sqrt{\left | i-j \right |}\)，现在，我们记这个值为\(f_j\)，且\(f_j\)是关于i的一个函数，\(i\geqslant j\)。那么，所有的\(f_j\)大概会长成这个样子：



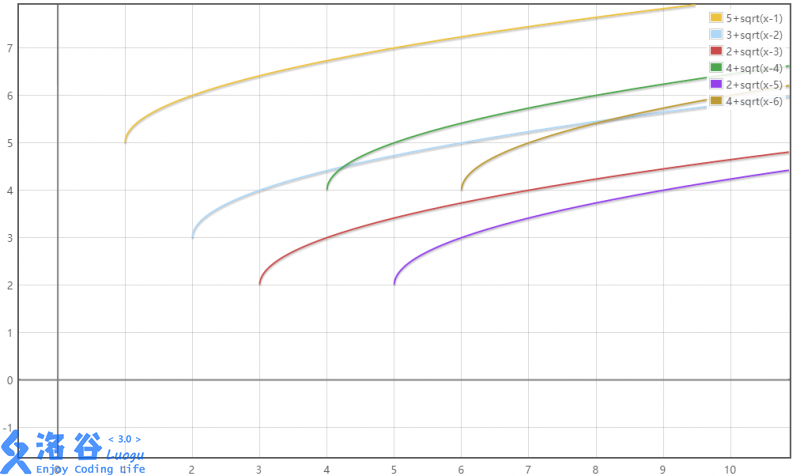
不难看出，每个\(f_j\)都是单调递增的，形状都是一样的（但定义域和值域不同），且斜率越来越小（这貌似叫上凸？）。



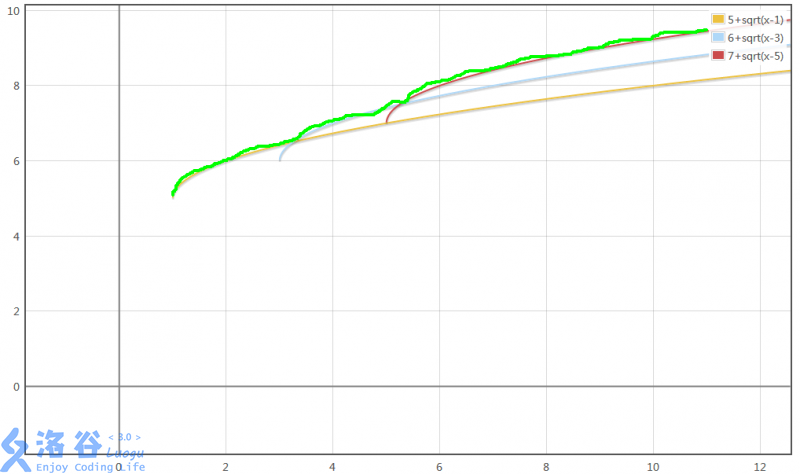
但是如果函数长成这张图那样，我们真正需要的只有上面的那一条绿线。

假设在程序中我们有了这张图，问题就变得hin简单，用最高的那个函数一算就可以辣（比如这张图就是上面那个黄色的）。

于是，问题转化为如何找出最高的那个\(f_j\)了。\(f_j\)还有一个很好的性质，就是对于最高的那个\(f_j\)，它的巅峰时期绝对是一段连续的区间（因为上凸嘛），且最高的那条一定是在某两条函数图像的交点处改变的。

然后，我们发现这个东西用单调队列很好维护，我们可以顺带求出i位置的答案。此处令\(cur\)为当前枚举到的\(j\)，\(q\)为单调队列(存的是\(j\))，\(h\)为队头指针，\(t\)为队尾指针，\(isx[i]\)为队列中第\(i\)个\(f_j\)与队列中第\(i+1\)个\(f_j\)的交点横坐标，\(intersectionX(i,j)\)返回的是\(f_i\)与\(f_j\)交点的横坐标。我们先按\(j\)从小到大把\(j\)加入，但我们要怎样维持队列的单调性呢？

1.当\(isx[t-1] \geqslant intersectionX(q[t],cur)\)时，那么就可以把\(q[t]\)弹出（想一想，画一下图就很清楚了）

2.把\(j\)插入到队尾

3.当\(isx[h] \leqslant cur\)时，那么就可以把\(q[h]\)弹出（显然嘛）

操作完后，\(q[h]\)就是我们要的最高的\(f_j\)的\(j\)了，然后我们就可以更新\(i\)位置的答案啦。

那么\(intersectionX(i,j)\)该怎样求呢？因为问题是定义在正整数域上的，我们就二分一下。

最后，注意一下砸，因为我们要从小到大加入j，而枚举点可能会在中间，所以我们要正着跑一遍，再倒着跑一遍，两遍取一下\(max\)。

上代码：

#include <bits/stdc++.h>

using namespace std;

#define re register
#define N 20000000

int n, isx[N+5], q[N+5], a[N+5];
double f[N+5];  //答案数组

double calc(int x, int y) { //计算a[y]+sqrt(x-y)
    return a[y]+sqrt(double(x)-y);
}

int intersection(int f1, int f2) {
    int l = 1, r = n, mid, ret = r+1; //ret要设成n+1，因为在1~n中可能没有交点
    while(l <= r) { //二分交点
        mid = (l+r)/2;
        if(calc(mid, f1) <= calc(mid, f2)) ret = mid, r = mid-1;
        else l = mid+1;
    }
    return ret;
}

void solve() {
    for(re int h = 1, t = 0, i = 1; i <= n; ++i) {
        while(h < t && isx[t-1] >= intersection(q[t], i)) --t; //队尾删除操作
        isx[t] = intersection(q[t], i), q[++t] = i; //插入到队尾
        while(h < t && isx[h] <= i) ++h; //队头弹出操作
        f[i] = max(f[i], calc(i, q[h])); //更新答案
    }
}

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n;
    for(re int i = 1; i <= n; ++i) cin >> a[i];
    solve();
    for(re int i = 1, j = n; i < j; ++i, --j) swap(a[i], a[j]), swap(f[i], f[j]); //反转序列
    solve();
    for(re int i = n; i >= 1; --i) cout << ceil(f[i])-a[i] << endl; //计算答案
    return 0;
}