HDU 3861 The King’s Problem 最小路径覆盖（强连通分量缩点+二分图最大匹配）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3861

最小路径覆盖的一篇博客：https://blog.csdn.net/qq_39627843/article/details/82012572

题意：

把城市至少分成几个块，规则有三
1. A能B，B能到A，那么A,B一定要在一起。
2. 一个城市只能属于一个块。 （说明了是最小不相交覆盖）
3. 在一个块里的城市，任意2点之间必须有路径。
对于规则1，就是说强连通的必须在一起，所以用Tarjan进行缩点，然后，规则2,3就是求DAG(有向无环图)最小路径覆盖。（最小路径覆盖=顶点数-最大匹配）

首先我们需要了解到最小覆盖路径的定义：通俗点将，就是在一个有向图中，找出最少的路径，使得这些路径经过了所有的点。

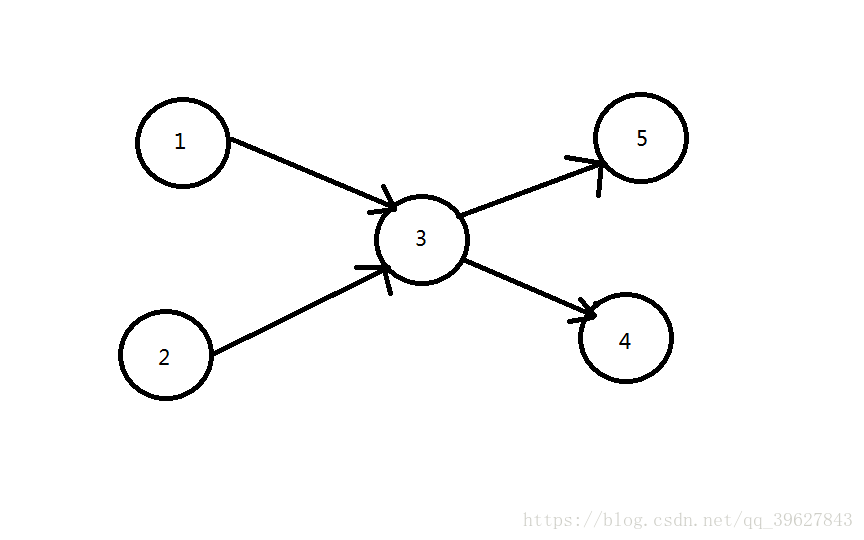
最小路径覆盖分为最小不相交路径覆盖和最小可相交路径覆盖。

最小不相交路径覆盖：每一条路径经过的顶点各不相同。如图，其最小路径覆盖数为3。即1->3>4，2，5。

最小可相交路径覆盖：每一条路径经过的顶点可以相同。如果其最小路径覆盖数为2。即1->3->4，2->3>5。

特别的，每个点自己也可以称为是路径覆盖，只不过路径的长度是0。

DAG的最小不相交路径覆盖

算法：把原图的每个点V拆成VxVx和VyVy两个点，如果有一条有向边A->B，那么就加边Ax−>ByAx−>By。这样就得到了一个二分图。那么最小路径覆盖=原图的结点数-新图的最大匹配数。

证明：一开始每个点都是独立的为一条路径，总共有n条不相交路径。我们每次在二分图里找一条匹配边就相当于把两条路径合成了一条路径，也就相当于路径数减少了1。所以找到了几条匹配边，路径数就减少了多少。所以有最小路径覆盖=原图的结点数-新图的最大匹配数。

因为路径之间不能有公共点，所以加的边之间也不能有公共点，这就是匹配的定义。

说的拆点这么高深，其实操作起来超级超级简单，甚至没有操作。

简单的来说，每个顶点都能当成二分图中作为起点的顶点。

至于为什么答案是 n-ans，我谈谈我的理解

用dfs求的ans表示的意思是匹配数，换句话说，就是一条路连着的路径上的点的个数-1

DAG的最小可相交路径覆盖

算法：先用floyd求出原图的传递闭包，即如果a到b有路径，那么就加边a->b。然后就转化成了最小不相交路径覆盖问题。

证明：为了连通两个点，某条路径可能经过其它路径的中间点。比如1->3->4，2->4->5。但是如果两个点a和b是连通的，只不过中间需要经过其它的点，那么可以在这两个点之间加边，那么a就可以直达b，不必经过中点的，那么就转化成了最小不相交路径覆盖。

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<stack>
using namespace std;

int head[5010], used[5010], head1[5010];
int dfn[5010], low[5010], vis[5010], color[5010];
int deep, cnt, cnt1, kinds_color, goal[5010];
stack<int>S;

struct Edge
{
	int to, next;
}edge[100010], edge1[100010];

void add(int a, int b) //存边
{
	edge[++ cnt].to = b;
	edge[cnt].next = head[a];
	head[a] = cnt;
}

void Add(int a, int b) //存缩点后的边
{
	edge1[++ cnt1].to = b;
	edge1[cnt1].next = head1[a];
	head1[a] = cnt1;
}

void tarjan(int now)
{
	dfn[now] = low[now] = ++ deep;
	S.push(now);
	vis[now] = 1;
	for(int i = head[now]; i != 0; i = edge[i].next)
	{
		int to = edge[i].to;
		if(!dfn[to])
		{
			tarjan(to);
			low[now] = min(low[now], low[to]);
		}
		else if(vis[to])
			low[now] = min(low[now], dfn[to]);
	}
	if(low[now] == dfn[now])
	{
		kinds_color ++;
		while(1)
		{
			int temp = S.top();
			S.pop();
			vis[temp] = 0;
			color[temp] = kinds_color;
			if(temp == now)
				break;
		}
	}
}

bool find(int x) //找最大匹配
{
	for(int i = head1[x]; i !=0; i = edge1[i].next)
	{
		int t = edge1[i].to;
		if(!used[t])
		{
			used[t] = 1;
			if(!goal[t] || find(goal[t]))
			{
				goal[t] = x;
				return true;
			}
		}
	}
	return false;
}

int main()
{
	int T, n, m;
	int a, b, ans;
	scanf("%d", &T);
	while(T --)
	{
		deep = cnt = kinds_color = cnt1 = ans = 0;
		memset(vis, 0, sizeof(vis));
		memset(dfn, 0, sizeof(dfn));
		memset(goal, 0, sizeof(goal));
		memset(low, 0, sizeof(low));
		memset(head, 0, sizeof(head));
		memset(head1, 0, sizeof(head1));
		scanf("%d%d", &n, &m);
		for(int i = 1; i <= m; i ++)
		{
			scanf("%d%d", &a, &b);
			add(a, b);
		}
		for(int i = 1; i <= n; i ++)
		{
			if(!dfn[i])
				tarjan(i);
		}
		for(int i = 1; i <= n; i ++)
		{
			for(int j = head[i]; j != 0; j = edge[j].next)
			{
				int to = edge[j].to;
				int x = color[i], y = color[to];
				if(x != y)
					Add(x, y);
			}
		}
		for(int i = 1; i <= kinds_color; i ++)
		{
			memset(used, 0 ,sizeof(used));
			if(find(i))
				ans ++;
		}
		printf("%d\n", kinds_color - ans);
	}
	return 0;
}