吴恩达老师机器学习课程chapter06——支持向量机与核函数

本文是非计算机专业新手的自学笔记，高手勿喷。

本文仅作速查备忘之用，对应吴恩达(AndrewNg)老师的机器学期课程第十二章。

吴恩达老师机器学习课程chapter06——支持向量机与核函数

支持向量机(support vector machine)是一种二类分类模型，其基本模型是在特征空间上的间隔最大的线性分类器，SVM的学习策略就是间隔最大化，又叫做大间距分类器。

和前面的内容一样，本章缺少更多数学推导，可做入门了解。

支持向量机

想要间隔最大化，我们希望有以下关系：

当y=1时，希望$h_{\theta}(x) \approx 1, \theta^Tx\gg 0 $
当y=0时，希望$h_{\theta}(x) \approx 0, \theta^Tx\ll 0$

可以用这种近似关系构建新的Cost函数得到新的J(θ)：

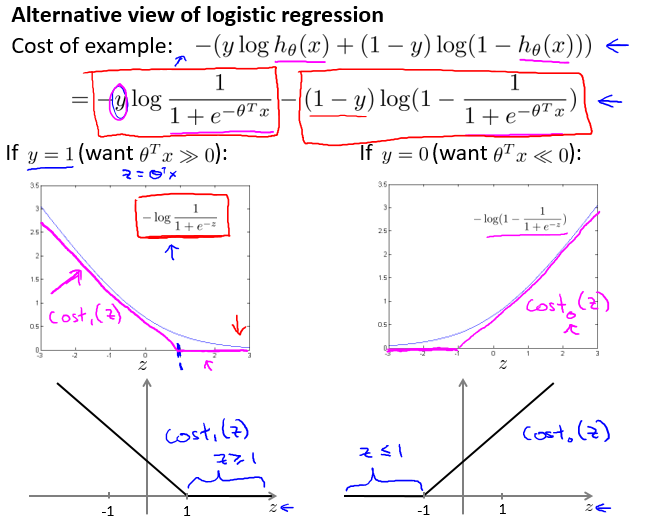
支持向量机的假设模型与J(θ)：

\[h_{\theta}(x)=\left\{\begin{array}{ll}
1 & \text { if } \theta^{T} x \geqslant 0 \\
0 & \text { otherwise }
\end{array}\right.
\]

\[\min _{\theta}J(\theta)=\min _{\theta} C \sum_{i=1}^{m}\left[y^{(i)} \operatorname{cost}_{1}\left(\theta^{T} x^{(i)}\right)+\left(1-y^{(i)}\right) \operatorname{cost}_{0}\left(\theta^{T} x^{(i)}\right)\right]+\frac{1}{2} \sum_{i=1}^{n} \theta_{j}^{2}
\]

当y=1时，希望 $\theta^Tx > 1 $
当y=0时，希望 $\theta^Tx＜ -1$

C很大时，对于判断错误的惩罚就很大，以至于：

\[J(\theta)=\frac{1}{2} \sum_{i=1}^{n} \theta_{j}^{2}
\]

向量内积的几何意义：

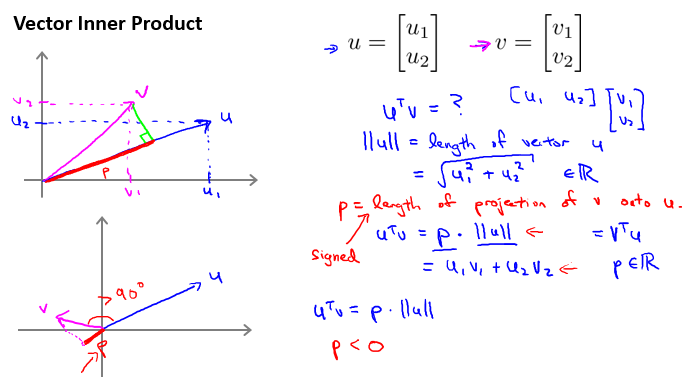
这里暂时没有给出严格证明。

但通过几何意义，可以直观感受SVM为什么能够使得间距最大。举例如下，考虑情况：$θ_0$=0，n=2，:

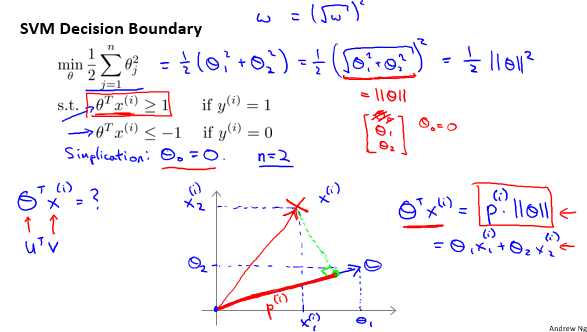
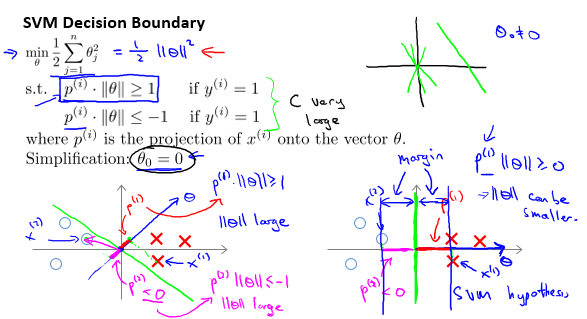
本例当中，坐标轴中，向量 $\theta$ (图中蓝线)与直线 $θ^Tx=0$(图中绿线)垂直。

各样本$x^{(i)}$在向量 $θ$ 上的投影为 $p^{(i)}$(图中红线)。

化使得$\|\theta\|$很小，那么$p^{(i)}$就变大，从而形成大间隔。

核函数(kernels)

对于非线性分类，其边界可能比较复杂，那么特征就比较多，假设模型就会比较复杂。

可以通过核函数，将输入空间映射到高维特征空间，不用计算复杂的非线性边界，使用线性平面就能获得完成分类。

选择一些标记点(landmark)，记作$l^{(i)}$；并选择如下的函数作为核函数，记作$f_i=similarity(x,l^{(i)})$，也被称为高斯核函数(gaussian kernel)：

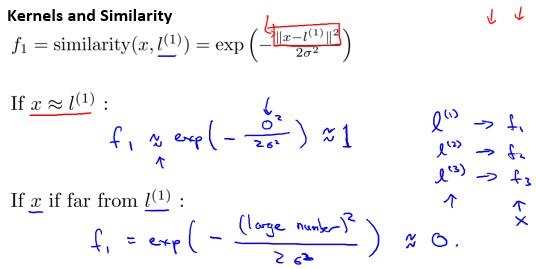
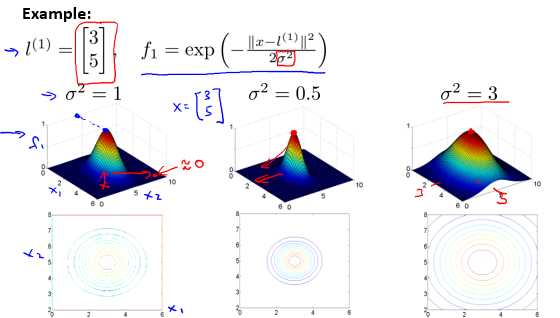
可以很清楚的看到，该核函数将二维平面中的点映射到了三维空间中。其中 $ \sigma ^{2} $ 越大，similarity函数越平整；反之越尖锐。在新的三维空间中，可以通过三维平面$\theta_{0}+\theta_{1} f_{1}+\theta_{2} f_{2}+\theta_{3} f_{3}=0$进行分类。

举例如下：

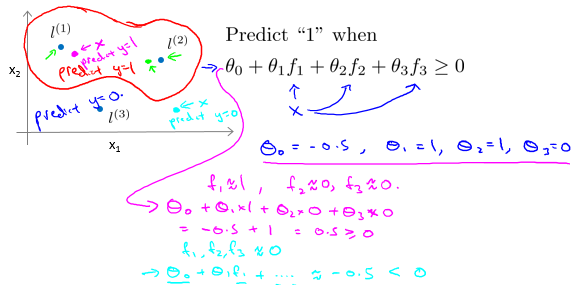
SVM与核函数的结合

已知有样本m个，特征n个，选择这m个样本$x^{(i)}$作为标记点$l^{(i)}$。

将1样本$x^{(i)}$和n个标记点$l^{(i)}$依次比较相似度，即计算$f_i=similarity(x^{(i)},l^{(i)})$，并每一次比较结果作为一个新特征，将其组成一个新的向量 f。和x向量中添加$x_0$对应的，在f中添加$f_0 =1(1与1的相似度为1)$。

其本质，是从原本的n+1维的特征的向量 x 转化为了 m+1维的新特征的向量 f。

这时候，最优问题也转变为了 f 的最优问题：

\[\min _{\theta} C \sum_{i=1}^{m} y^{(i)} \operatorname{cost}_{1}\left(\theta^{T} f^{(i)}\right)+
\left(1-y^{(i)}\right) \operatorname{cost}_{0}\left(\theta^{T} f^{(i)}\right)
+\frac{1}{2} \sum_{j=1}^{m} \theta_{j}^{2}
\]

同样的，$theta_0$不参与正则化。（吴老师ppt上的公式正则项求和符号上方有误）

接下来再用支持向量机的思路解决这个分类问题即可。