P2295 MICE 网格中的DP

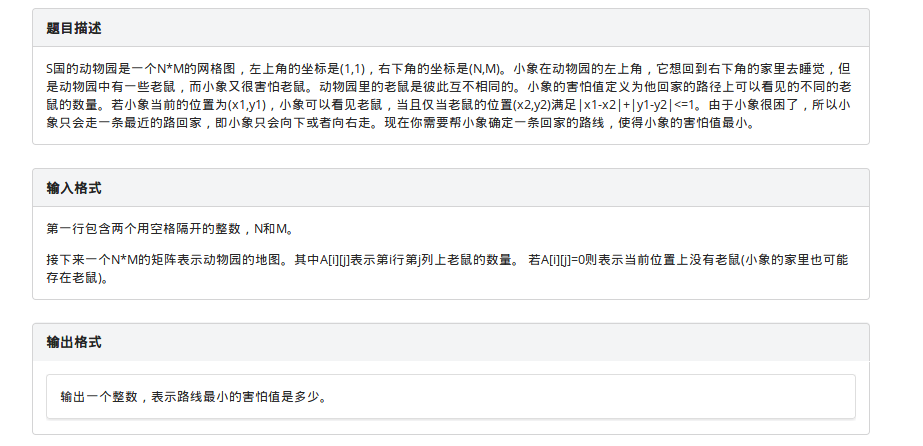
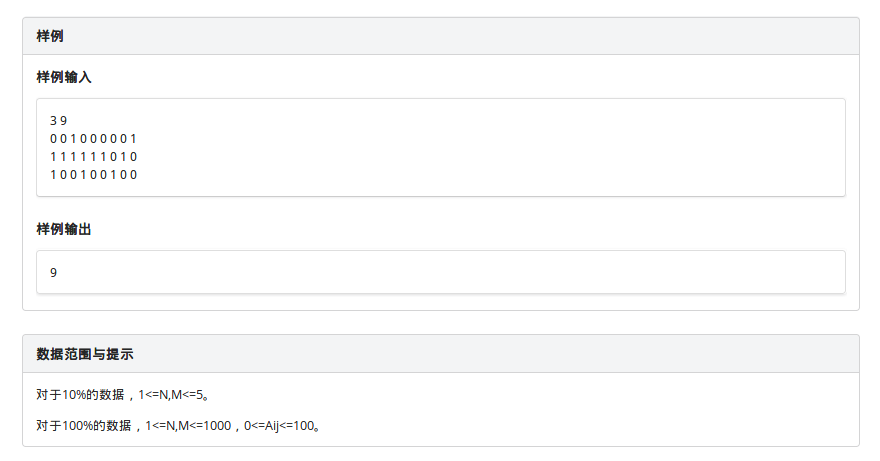
题目描述

分析

很好的一道网格中的\(DP\)题

我们设\(f[x][y]\)为小象到达坐标为\((x,y)\)的点时看到的最少的老鼠的数量

但是这样定义是不好转移的，因为小象可能从上面的格子转移下来，也可能从上面的格子转移过来

所以我们用三维数组记录状态，我们设\(f[x][y][0]\)为当前格子从正上方的格子转移过来所看到的最少的老鼠的数量

\(f[x][y][1]\)为当前格子从正左方的格子转移过来所看到的最少的老鼠的数量

我们来分情况讨论一下

无非是考虑当前的位置和当前上下左右的\(4\)个格子，去一下重

1、当前格子从正上方转移过来，当前格子正上方的格子也由正上方的格子转移过来

此时当前格子的价值\(a[i][j]\)已经在\(f[i-1][j][0]\)中计算过

而当前格子正上方的格子的价值\(a[i-1][j]\)已经在\(f[i-2][j][0]\)或\(f[i-2][j][1]\)中计算过

\[f[i][j][0]=min(f[i][j][0],f[i-1][j][0]+a[i][j-1]+a[i][j+1]+a[i+1][j]);
\]

2、当前格子从正上方转移过来，当前格子正上方的格子由正左方的格子转移过来

此时当前格子的价值\(a[i][j]\)已经在\(f[i-1][j][1]\)中计算过

当前格子正左方格子的价值\(a[i][j-1]\)已经在\(f[i-1][j-1][1]\)或\(f[i-1][j-1][0]\)中计算过

当前格子正上方格子的价值\(a[i-1][j]\)也已经在\(f[i-1][j-1][1]\)或\(f[i-1][j-1][0]\)中计算过

\[f[i][j][0]=min(f[i][j][0],f[i-1][j][1]+a[i][j+1]+a[i+1][j]);
\]

3、当前格子从正左方转移过来，当前格子正左方的格子也由正左方的格子转移过来

此时当前格子的价值\(a[i][j]\)已经在\(f[i][j-1][1]\)中计算过

当前格子正左方格子的价值\(a[i][j-1]\)已经在\(f[i][j-2][1]\)或\(f[i][j-2][0]\)中计算过

\[f[i][j][1]=min(f[i][j][1],f[i][j-1][1]+a[i-1][j]+a[i][j+1]+a[i+1][j]);
\]

4、当前格子从正左方转移过来，当前格子正左方的格子由正上方的格子转移过来

此时当前格子的价值\(a[i][j]\)已经在\(f[i][j-1][0]\)中计算过

当前格子正左方格子的价值\(a[i][j-1]\)已经在\(f[i-1][j-1][1]\)或\(f[i-1][j-1][0]\)中计算过

当前格子正上方格子的价值\(a[i-1][j]\)也已经在\(f[i-1][j-1][1]\)或\(f[i-1][j-1][0]\)中计算过

\[f[i][j][1]=min(f[i][j][1],f[i][j-1][0]+a[i][j+1]+a[i+1][j]);
\]

要注意初始化

\[f[1][1][0]=f[1][1][1]=a[1][1]+a[1][2]+a[2][1];
\]

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1055;
int a[maxn][maxn],f[maxn][maxn][3];
int main(){
    memset(f,0x3f,sizeof(f));
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
        }
    }
    f[1][1][0]=f[1][1][1]=a[1][1]+a[1][2]+a[2][1];
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            f[i][j][0]=min(f[i][j][0],f[i-1][j][0]+a[i][j-1]+a[i][j+1]+a[i+1][j]);
            f[i][j][0]=min(f[i][j][0],f[i-1][j][1]+a[i][j+1]+a[i+1][j]);
            f[i][j][1]=min(f[i][j][1],f[i][j-1][1]+a[i-1][j]+a[i][j+1]+a[i+1][j]);
            f[i][j][1]=min(f[i][j][1],f[i][j-1][0]+a[i][j+1]+a[i+1][j]);
        }
    }
    printf("%d\n",min(f[n][m][0],f[n][m][1]));
    return 0;
}