PAT甲级——A1135 Is It A Red-Black Tree 【30】

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

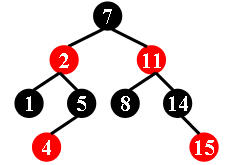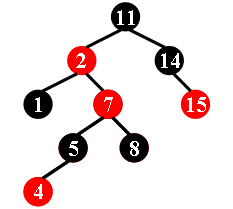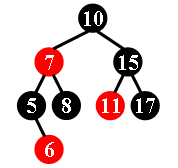Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Sample Output:

Yes
No
No

【注意，不用判断是不是平衡二叉树，因为红黑树不是严格的平衡二叉树】
分析：判断以下几点：
1.根结点是否为黑色 
2.如果一个结点是红色，它的孩子节点是否都为黑色 
3.从任意结点到叶子结点的路径中，黑色结点的个数是否相同
所以分为以下几步：
0. 根据先序建立一棵树，用链表表示
1. 判断根结点（题目所给先序的第一个点即根结点）是否是黑色
2. 根据建立的树，从根结点开始遍历，如果当前结点是红色，判断它的孩子节点是否为黑色，递归返回结果
3. 从根节点开始，递归遍历，检查每个结点的左子树的高度和右子树的高度（这里的高度指黑色结点的个数），比较左右孩子高度是否相等，递归返回结果

 #include <iostream>
 #include <vector>
 #include <cmath>
 #include <algorithm>
 using namespace std;
 struct Node
 {
     int val;
     Node *l, *r;
     Node(int a) :val(a), l(nullptr), r(nullptr) {}
 };
 int n, m;
 int getHigh(Node *root)//是指黑节点个数哦
 {
     if (root == nullptr)
         return ;
     int ln = getHigh(root->l);
     int rn = getHigh(root->r);
     return root->val >  ? max(ln, rn) +  : max(ln, rn);//计算黑节点个数
 }
 Node *Insert(Node *root, int x)
 {
     if (root == nullptr)
         root = new Node(x);
     else if (abs(x) < abs(root->val))
         root->l = Insert(root->l, x);
     else
         root->r = Insert(root->r, x);
     return root;
 }
 bool redNode(Node *root)
 {
     if (root == nullptr)
         return true;
     if (root->val < )//红节点孩子一定要是黑节点
         if (root->l != nullptr && root->l->val <  ||
             root->r != nullptr && root->r->val < )
             return false;
     return redNode(root->l) && redNode(root->r);
 }
 bool balanceTree(Node *root)
 {
     if (root == nullptr)        return true;
     if (getHigh(root->l) != getHigh(root->r))return false;//黑节点个数不同
     return balanceTree(root->l) && balanceTree(root->r);
 }
 int main()
 {
     int n, m;
     cin >> n;
     while (n--)
     {
         cin >> m;
         vector<int>v(m);
         Node *root = nullptr;
         for (int i = ; i < m; ++i)
         {
             cin >> v[i];
             root = Insert(root, v[i]);
         }
         if (v[] >=  && balanceTree(root) && redNode(root))
             cout << "Yes" << endl;
         else
             cout << "No" << endl;
     }
     return ;
 }