[离散时间信号处理学习笔记] 7. z变换

z变换及其收敛域

回顾前面的文章，序列$x[n]$的傅里叶变换（实际上是DTFT，由于本书把它叫做序列的傅里叶变换，因此这里以及后面的文章也统一称DTFT为傅里叶变换）被定义为

$X(e^{j\omega}) = \displaystyle{ \sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n} }$

序列$x[n]$的z变换被定义成

$X(z) = \displaystyle{ \sum_{n=-\infty}^{\infty}x[n]z^{-n} }$

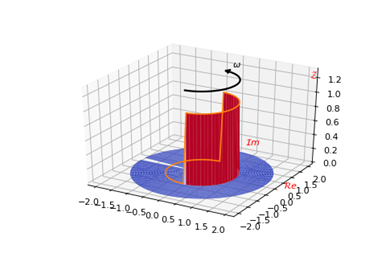
其中$z$就是一个复数变量，可见$z$变换与傅里叶变换一样把序列变成了函数。复变量$z$可以表示形式$z=|z|e^{j\omega}=re^{j\omega}$，代入z变换变成

$X(z) = \displaystyle{ \sum_{n=-\infty}^{\infty}x[n]r^{-n}e^{-j\omega n} }$

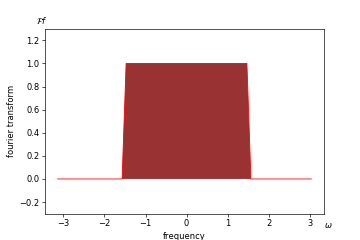
可以发现傅里叶变换就是$r=1$的z变换。

 

要使得z变换有意义，那么变换所得的函数必须在有限处收敛，即

$\begin{align*}
|X(z)|&= \left|\sum_{n=-\infty}^{\infty}x[n]r^{-n}e^{-j\omega n}\right|\\
&<\sum_{n=-\infty}^{\infty}|x[n]|r^{-n} \\
&=x[0]+ \sum_{n=1}^{\infty}|x[n]|(r^{-1})^n+\sum_{n=1}^{\infty}|x[-n]|r^n <\infty
\end{align*}$

按照root test，需要满足以下条件才能使得函数收敛

$\left\{\begin{matrix}
\displaystyle{ \limsup_{n\to\infty}|x[n]|^{\frac{1}{n}}r^{-1} < 1 }\\
\displaystyle{ \limsup_{n\to\infty}|x[-n]|^{\frac{1}{n}}r < 1 }
\end{matrix}\right.$

即

$\left\{\begin{matrix}
r &> &\displaystyle{\lim_{n\to\infty} |x[n]|^{\frac{1}{n}}} \\
r &< &\displaystyle{\lim_{n\to\infty} |x[-n]|^{\frac{1}{-n}}}
\end{matrix}\right.$

观察上面的不等式，可以发现z变换的收敛可以分为五种

• $x[n]$是右边序列，即序列在$n<N_1<\infty$处全为0，那么该序列的收敛域就是从极点（使得函数趋于$\pm\infty$的点）往外延伸到$z=\pm\infty$
• $x[n]$是左边序列，即序列在$n>N_2>-\infty$处全为0 ，那么该序列的收敛域就是从极点向内延伸至$z=0$
• $x[n]$是双边序列，把该序列分成右边序列与左边序列后，如果这两个序列的z变换的收敛域有重合的部分，则该序列z变换的收敛域呈圆环状
• $x[n]$是双边序列，把该序列分成右边序列与左边序列后，如果这两个序列的z变换的收敛域没有重合的部分，则该序列z变换不存在收敛域
• $x[n]$是有限长序列，那么该序列的z变换必定在有限的范围内收敛

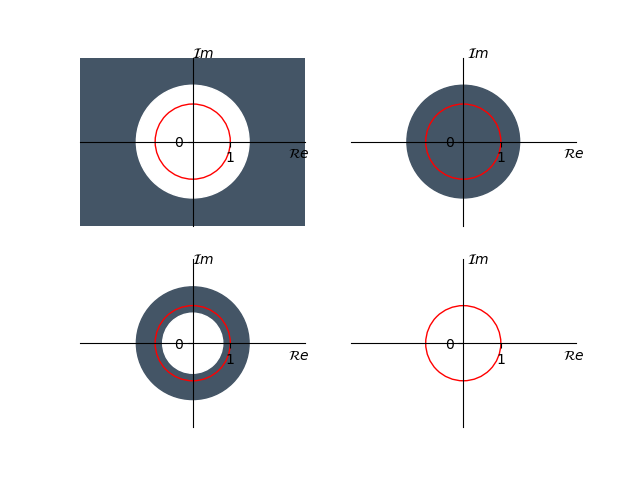
图中阴影部分为收敛域，其中红色圆圈是$|z| = r = 1$，即傅里叶变换，如果z变换的收敛域包含$r=1$的圆圈，就表明该序列的傅里叶变换收敛。

z变换例子

考虑一个为两个实指数和的信号

$x[n] = \left(\frac{1}{2}\right)^n u[n]+\left(-\frac{1}{3}\right)^n u[n]$

其z变换为

$\begin{align*}
X(z) &= \sum_{n=-\infty}^{\infty}\left\{ \left(\frac{1}{2} \right )^n u[n]+\left(-\frac{1}{3} \right )^n u[n] \right \}z^{-n}\\
&=\sum_{n=-\infty}^{\infty}\left(\frac{1}{2} \right )^n u[n]z^{-n}+\sum_{n=-\infty}^{\infty}\left(-\frac{1}{3} \right )^n u[n]z^{-n}\\
&=\sum_{n=0}^{\infty}\left(\frac{1}{2}z^{-1} \right )^n +\sum_{n=0}^{\infty}\left(-\frac{1}{3}z^{-1} \right )^n \\
&=\frac{1}{1-\frac{1}{2}z^{-1}}+\frac{1}{1+\frac{1}{3}z^{-1}} \quad Geometric\ Series\\
&=\frac{2z\left(z-\frac{1}{12} \right )}{\left(z-\frac{1}{2} \right )\left(z+\frac{1}{3} \right )}
\end{align*}$

为了使z变换收敛，必须满足条件

$\left\{\begin{matrix}
\left| \frac{1}{2}z^{-1}\right|&<&1\\
\left| -\frac{1}{3}z^{-1}\right|&<&1
\end{matrix}\right.$

即

$\left\{\begin{matrix}
\left| z\right|&>&\frac{1}{2}\\
\left| z\right|&>&\frac{1}{3}
\end{matrix}\right.$

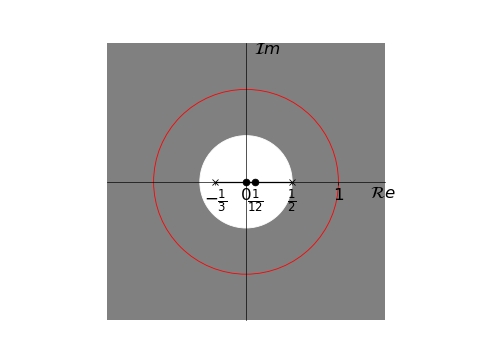
由此可得到收敛域为$|z|>\frac{1}{2}$。观察z变换的结果，可以发现：

当$z=\frac{1}{2}$或者$z=-\frac{1}{3}$时，z变换趋于无穷，因此这两个点为极点

当$z=0$或者$z=\frac{1}{12}$时，z变换为0，因此这两个点为零点