二叉树学习笔记之二叉查找树（BSTree）

二叉查找树即搜索二叉树，或者二叉排序树（BSTree），学习回顾一下有关的知识。

>>关于二叉查找树

二叉查找树（Binary Search Tree）是指一棵空树或者具有下列性质的二叉树：
1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉查找树。
4. 没有键值相等的节点，这个特征很重要，可以帮助理解二叉排序树的很多操作。
二叉查找树具有很高的灵活性，对其优化可以生成平衡二叉树，红黑树等高效的查找和插入数据结构。

>>基本性质

（1）二叉查找树是一个递归的数据结构，对二叉查找树进行中序遍历，可以得到一个递增的有序序列。
（2）二叉查找树上基本操作的执行时间和树的高度成正比。

对一棵n个节点的完全二叉树来说，树的高度为lgn，这些操作的最坏情况运行时间为O(lg n)，而如果是线性链表结构，这些操作的最坏运行时间是O(n)。
一棵随机构造的二叉查找树的期望高度为O(lg n)，但实际中并不能总是保证二叉查找树是随机构造的，
有些二叉查找树的变形能保证各种基本操作的最坏情况性能，比如红黑树的高度为O(lg n)，而B树对维护随机访问的二级存储器上的数据库特别有效。

注意对复杂度的理解，所谓的O(lg n)就是指复杂度是对数级别，是数量级的比较，和对数的底数其实没关系，

只要底数是大于1的，就是相同的数量级，有些书上说二叉查找树的复杂度是O(log2-n)，指的是相同的时间复杂度。

>>前驱和后继节点

一个节点的后继是该节点的后一个，即比该节点键值稍大的节点。
给定一个二叉查找树中的节点，找出在中序遍历顺序下某个节点的前驱和后继。
如果树中所有关键字都不相同，则某一节点x的前驱就是小于key[x]的所有关键字中最大的那个节点，后继即是大于key[x]中的所有关键字中最小的那个节点。根据二叉查找树的结构和性质，不用对关键字做任何比较，就可以找到某个节点的前驱和后继。

>>查找、插入与删除

（1）查找
利用二叉查找树左小右大的性质，可以很容易实现查找任意值和最大/小值。

在二叉查找树中查找一个给定的关键字k的过程与二分查找很类似，

首先是关键字k与树根的关键字进行比较，如果k比根的关键字大，则在根的右子树中查找，否则在根的左子树中查找，重复此过程，直到找到与遇到空节点为止。

在二叉查找树中查找x的过程如下：
1.若二叉树是空树，则查找失败。
2.若x等于根节点的数据，则查找成功，否则。
3.若x小于根节点的数据，则递归查找其左子树，否则。
4.递归查找其右子树。

（2）插入
二叉树查找树b插入操作x的过程如下：
1.若b是空树，则直接将插入的节点作为根节点插入。
2.x等于b的根节点的数据的值，则直接返回，否则。
3.若x小于b的根节点的数据的值，则将x要插入的节点的位置改变为b的左子树，否则。
4.将x要出入的节点的位置改变为b的右子树。

（3）删除

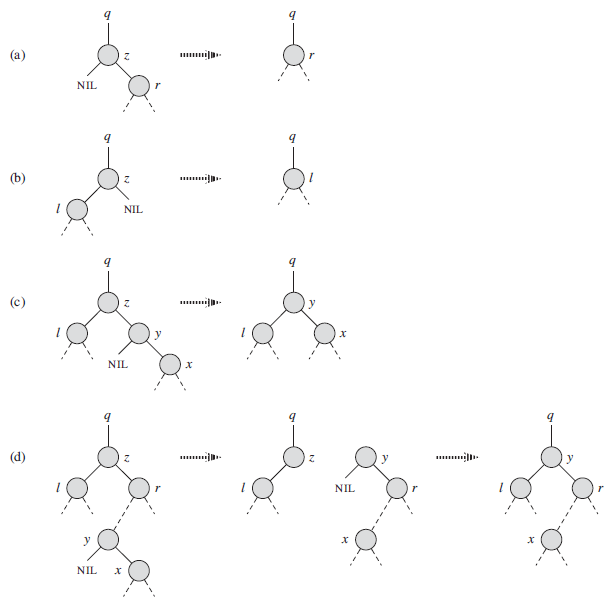
假设从二叉查找树中删除给定的结点z，分三种情况讨论：
1.节点z为叶子节点，没有孩子节点，那么直接删除z，修改父节点的指针即可。
2.节点z只有一个子节点或者子树，将节点z删除，根据二叉查找树的性质，将z的父节点与子节点关联就可以了。
3.节点Z有两个子节点，删除Z该怎样将Z的父结点与这两个孩子结点关联呢？
在删去节点Z之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整。
这种情况下可以用Z的后继节点来替代Z。
实现方法就是将后继从二叉树中删除，将后继的数据覆盖到Z中。

>>代码实现

主要参考《数据结构与算法分析—Java语言实现》：

public class BinarySearchTree <T extends Comparable<? super T>>{

	//节点数据结构 静态内部类
	static class BinaryNode<T>{
		T data;
		BinaryNode<T> left;
		BinaryNode<T> right;
		public BinaryNode(){
			data=null;
		}
		public BinaryNode(T data) {
			this(data,null,null);
		}
		public BinaryNode(T data,BinaryNode<T> left,BinaryNode<T> right){
			this.data=data;
			this.left=left;
			this.right=right;
		}
	}

	//私有的头结点
	private BinaryNode<T> root;

	//构造一棵空二叉树
	public BinarySearchTree(){
		root=null;
	}
	//二叉树判空
	public boolean isEmpty(){
		return root==null;
	}
	//清空二叉树
	public void clear(){
		root=null;
	}

	//检查某个元素是否存在
	public boolean contains(T t){
		return contains(t,root);
	}

	/**
	 * 从某个节点开始查找某个元素是否存在
	 * 在二叉查找树中查找x的过程如下：
	 * 1、若二叉树是空树，则查找失败。
	 * 2、若x等于根结点的数据，则查找成功，否则。
	 * 3、若x小于根结点的数据，则递归查找其左子树，否则。
	 * 4、递归查找其右子树。
	 */
	public boolean contains(T t,BinaryNode<T> node){
		if(node==null){
			return false;
		}
		/**
		 * 这就是为什么使用Comparable的泛型
		 * compareTo的对象也必须是实现了Comparable接口的泛型,
		 * 所以参数必须是BinaryNode<T> node格式
		 */
		int result=t.compareTo(node.data);
		if(result>0){//去右子树查找
			return contains(t,node.right);
		}else if(result<0){//去左子树查找
			return contains(t,node.left);
		}else{
			return false;
		}
	}

	//插入元素
	public void insert(T t){
		root=insert(t,root);
	}

	/**
	 * 将节点插入到以某个节点为头的二叉树中
	 * 这个插入其实也是一个递归的过程
	 * 递归最深层的返回结果一个包含要插入的节点子树的头节点
	 */
	public BinaryNode insert(T t,BinaryNode<T> node){
		//如果是空树，直接构造一棵新的二叉树
		if(node==null){
			return new BinaryNode<T>(t);
		}

		int result=t.compareTo(node.data);

		if(result<0){
			node.left=insert(t,node.left);
		}else if(result>0){
			node.right=insert(t,node.right);
		}else{
			;//即要插入的元素和头节点值相等，直接返回即可
		}
		return node;
	}

	/**
	 * 删除元素
	 * 返回调整后的二叉树头结点
	 */
	public BinaryNode delete(T t){
		return delete(t,root);

	}

	/**
	 * 在以某个节点为头结点的树结构中删除元素
	 * 首先需要找到该关键字所在的节点p，然后具体的删除过程可以分为几种情况：
	 * p没有子女，直接删除p
	 * p有一个子女，直接删除p
	 * p有两个子女，删除p的后继q（q至多只有一个子女）
	 * 确定了要删除的节点q之后，就要修正q的父亲和子女的链接关系，
	 * 然后把q的值替换掉原先p的值，最后把q删除掉
	 */
	public BinaryNode delete(T t,BinaryNode<T> node){
		if(node==null){//节点为空还要啥自行车
			return node;
		}
		/**
		 * 首先要找到这个节点，所以还是得比较
		 */
		int result=t.compareTo(node.data);

		/**
		 * 去左半部分找这个节点，
		 * 找到节点result==0,这个递归就停止
		 */
		if(result<0){
			node.left=delete(t,node.left);
		}else if(result>0){//去右半部分找这个节点
			node.right=delete(t,node.right);
		}
		/**
		 * 如果这个节点的左右孩子都不为空，那么找到当前节点的后继节点，
		 *
		 */
		if(node.left!=null && node.right!=null){
			/**
			 * node节点的右子树部分的最小节点，实际上就是它的后继节点
			 * 得到后继节点的值
			 */
			node.data = findMin(node.right).data;
			/**
			 * 这个过程并不是删除后继节点，是一步一步的把所有的节点都替换上来
			 */
	        node.right = delete(node.data,node.right);
		}else{
			/**
			 * 如果二叉搜索树中一个节点是完全节点，
			 * 那么它的前驱和后继节点一定在以它为头结点的子树中，应该是这样的
			 * 来到了只有一个头节点和一个子节点的情况
			 */
			node = (node.left!=null)?node.left:node.right;
		}
		//此处的node，是经过调整后的传入的root节点
		return node;

	}

	/**
	 * 返回二叉树中的最小值节点
	 * 此时无比想念大根堆和小根堆
	 */
	public BinaryNode<T> findMin(BinaryNode node){
		if(node==null)
			return null;
		/**
		 * 如果node不为空，就递归的去左边找
		 * 最小值节点肯定是左孩子为空的节点
		 */
		if(node.left!=null)
			node=findMin(node.left);
		return node;
	}

}

　　

参考《算法导论》、

《数据结构与算法分析—Java语言实现》 

二叉查找树、维基百科、