Tukey法

在介绍Tukey方法前，首先了解学生化极差分布。

在概率论和统计学中，学生化极差分布是极差的抽样分布。该分布是一种连续型概率分布，用于在样本量较小且总体标准差未知的情况下估计正态分布总体的极差。

假设要比较的组数为k，那么在零假设成立的条件下，下面的随机变量服从学生化极差分布。

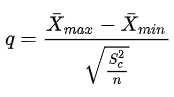
Tukey法的更多相关文章

  1. Bonferroni校正法

    Bonferroni校正:如果在同一数据集上同时检验n个独立的假设,那么用于每一假设的统计显著水平,应为仅检验一个假设时的显著水平的1/n http://baike.baidu.com/view/12 ...

  2. SAS学习笔记26 方差分析

    对于多于两组(k>2)样本均数的比较,t检验不再适用,方差分析(analysis of variance, ANOVA)则是解决上述问题的重要分析方法.方差分析由R.A.Fisher(1923) ...

  3. 《构建之法》阅读有疑 与 个人Week1作业

    <构建之法>阅读有疑 在用将近五节课的时间将邹欣老师的书<构建之法——现代软件工程>第二版大致看完.虽然全书是以轻松的口吻与”移山公司”员工的一些趣味谈话来传输一些理念和思想的 ...

  4. SAGE|DNA微阵列|RNA-seq|lncRNA|scripture|tophat|cufflinks|NONCODE|MA|LOWESS|qualitile归一化|permutation test|SAM|FDR|The Bonferroni|Tukey's|BH|FWER|Holm's step-down|q-value|

    生物信息学-基因表达分析 为了丰富中心法则,研究人员使用不断更新的技术研究lncRNA的方方面面,其中技术主要是生物学上的微阵列芯片技术和表达数据分析方法,方方面面是指lncRNA的位置特征. Bac ...

  5. SE_Work1_阅读构建之法&项目管理实践

    项目 内容 课程:北航-2020-春-软件工程 博客园班级博客 要求:阅读<构建之法>并回答问题 个人博客作业 我在这个课程的目标是 提升团队管理及合作能力,开发一项满意的工程项目 这个作 ...

  6. [C#] 软硬结合第二篇——酷我音乐盒的逆天玩法

    1.灵感来源: LZ是纯宅男,一天从早上8:00起一直要呆在电脑旁到晚上12:00左右吧~平时也没人来闲聊几句,刷空间暑假也没啥动态,听音乐吧...~有些确实不好听,于是就不得不打断手头的工作去点击下 ...

  7. 0-1背包问题蛮力法求解（c++版本）

    // 0.1背包求解.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include <iostream>   #define ...

  8. 算法笔记_013:汉诺塔问题（Java递归法和非递归法）

    目录 1 问题描述 2 解决方案  2.1 递归法 2.2 非递归法 1 问题描述 Simulate the movement of the Towers of Hanoi Puzzle; Bonus ...

  9. Matlab slice方法和包络法绘制三维立体图

    前言:在地球物理勘探,流体空间分布等多种场景中,定位空间点P(x,y,x)的物理属性值Q,并绘制三维空间分布图,对我们洞察空间场景有十分重要的意义. 1. 三维立体图的基本要件: 全空间网格化 网格节 ...

随机推荐

  1. CodeForces - 748D Santa Claus and a Palindrome (贪心+构造)

    题意:给定k个长度为n的字符串,每个字符串有一个魅力值ai,在k个字符串中选取字符串组成回文串,使得组成的回文串魅力值最大. 分析: 1.若某字符串不是回文串a,但有与之对称的串b,将串a和串b所有的 ...

  2. POJ - 3657 Haybale Guessing（二分+并查集）

    题意:有N个大小各不相同的点,给定Q个询问,格式为q1,q2,A,表示区间q1~q2的最小值是A,问第一个与之前询问结果出现冲突的询问. 分析: 1.二分询问的标号mid,查询1~mid是否出现询问冲 ...

  3. 转载电子发烧友网---STM32的IO口灌入电流和输出驱动电流

    刚开始学习一款单片机的时候一般都是从操作IO口开始的,所以我也一样,先是弄个流水灯. 刚开始我对STM32的认识不够,以为是跟51单片机类似,可以直接操作端口,可是LED灯却没反应,于是乎,仔细查看资 ...

  4. offsetof宏与container_of宏

    offsetof宏与container_of宏1.由结构体指针进而访问各元素的原理(1)通过结构体整体变量来访问其中各个元素,本质上是通过指针方式来访问的,形式上是通过.的方式来访问的(这个时候其实是 ...

  5. LINUX文件目录存放文件说明

    /bin bin是Binary的缩写.这个目录存放着最经常使用的命令. /boot这里存放的是启动Linux时使用的一些核心文件,包括一些连接文件以及镜像文件. /dev dev是Device(设备) ...

  6. win10编译libpng

    libpng在windows的编译. ligpng的官网介绍如下: libpng is the official PNG reference library. It supports almost a ...

  7. HDU 3484 Matrix Game 枚举暴力

    上次周赛碰到这个题目,居然都没思路,真是不应该啊,起码也应该想到枚举法. 因为题目只允许每一row进行reverse操作,而每两列可以进行交换操作,所以首先把row的变化固定下来,即枚举第一列与第1- ...

  8. kaggle——TMDB 电影票房收入预测

    介绍 看电影是目前人们休闲娱乐,消遣时光的选择之一.我们都知道,有些电影的票房很高,有的电影票房却很低,那么决定票房的因素是什么呢?本次将介绍,如何根据电影上映前的一些信息来预测出该电影的票房. 知识 ...

  9. 浅copy

    person=['aaa',['a',bbb'] p1=copy.copy(person) p2=person[:] p3=list(person) p4=person.copy() print(ty ...

  10. Luogu P3031 高于中位数

    定义序列\(x_i = f([H_i >=x])\;\;\;\;其中f(0) = -1,f(1) = 1\),那么区间[i,j]满足条件当且仅当sum_j-sum_{i-1} > 0,即s ...