verilog乘法器的设计

在verilog编程中，常数与寄存器变量的乘法综合出来的电路不同于寄存器变量乘以寄存器变量的综合电路。知乎里的解释非常好https://www.zhihu.com/question/45554104，总结乘法器模块的实现https://blog.csdn.net/yf210yf/article/details/70156855

乘法的实现是移位求和的过程

乘法器模块的实现主要有以下三种方法

1.串行实现方法

占用资源最多，需要的时钟频率高些，但是数据吞吐量却不大

两个N位二进制数x、y的乘积用简单的方法计算就是利用移位操作来实现。

其框图如下：

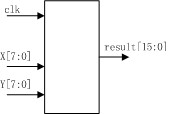
其状态图如下：

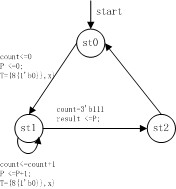
代码：

module multi_CX(clk, x, y, result);

    input clk;

    input [:] x, y;

    output [:] result;

    reg [:] result;

    parameter s0 = , s1 = , s2 = ;

    reg [:] count = ;

    reg [:] state = ;

    reg [:] P, T;

    reg [:] y_reg;

    always @(posedge clk) begin

        case (state)

            s0: begin

                count <= ;

                P <= ;

                y_reg <= y;

                T <= {{{'b0}}, x};

                state <= s1;

            end

            s1: begin

                if(count == 'b111)

                    state <= s2;

                else begin

                    if(y_reg[] == 'b1)

                        P <= P + T;

                    else

                        P <= P;

                    y_reg <= y_reg >> ;

                    T <= T << ;

                    count <= count + ;

                    state <= s1;

                end

            end

            s2: begin

                result <= P;

                state <= s0;

            end

            default: ;

        endcase

    end

endmodule

慢速信号处理中常用到的。

2.并行流水线实现方法

将操作数的N位并行提交给乘法器，这种方法并不是最优的实现架构，在FPGA中进位的速度远大于加法的速度，因此将相临的寄存器相加，相当于一个二叉树的结构，实际上对于n位的乘法处理，需要logn级流水来实现。

一个8位乘法器，其原理图如下图所示:

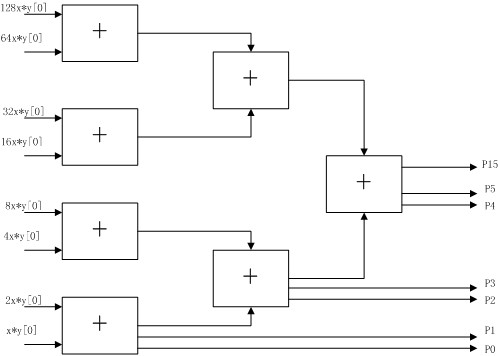
其实现的代码如下：

module multi_4bits_pipelining(mul_a, mul_b, clk, rst_n, mul_out);
input [:] mul_a, mul_b;
input  clk;
input  rst_n;
output [:] mul_out;

reg [:] mul_out;
reg [:] stored0;
reg [:] stored1;
reg [:] stored2;
reg [:] stored3;
reg [:] stored4;
reg [:] stored5;
reg [:] stored6;
reg [:] stored7;

reg [:] mul_out01;
reg [:] mul_out23;

reg [:] add01;
reg [:] add23;
reg [:] add45;
reg [:] add67;

always @(posedge clk or negedge rst_n) begin
    if(!rst_n) begin
mul_out <= ;
        stored0 <= ;
        stored1 <= ;
stored2 <= ;
stored3 <= ;
stored4 <= ;
        stored5 <= ;
stored6 <= ;
stored7 <= ;

add01 <= ;
add23 <= ;
add45 <= ;
add67 <= ;
    end
else begin
stored0 <= mul_b[]? {'b0, mul_a} : 16'b0;
stored1 <= mul_b[]? {'b0, mul_a, 1'b0} : 'b0;
stored2 <= mul_b[]? {'b0, mul_a, 2'b0} : 'b0;
stored3 <= mul_b[]? {'b0, mul_a, 3'b0} : 'b0;
stored4 <= mul_b[]? {'b0, mul_a, 4'b0} : 'b0;
stored5 <= mul_b[]? {'b0, mul_a, 5'b0} : 'b0;
stored6 <= mul_b[]? {'b0, mul_a, 6'b0} : 'b0;
stored7 <= mul_b[]? {'b0, mul_a, 7'b0} : 'b0;
add01 <= stored1 + stored0;
add23 <= stored3 + stored2;
add45 <= stored5 + stored4;
add67 <= stored7 + stored6;

mul_out01 <= add01 + add23;
mul_out23 <= add45 + add67;

mul_out <= mul_out01 + mul_out23;

    end
end
endmodule

流水线乘法器比串行乘法器的速度快很多很多，在非高速的信号处理中有广泛的应用。至于高速信号的乘法一般需要利用FPGA芯片中内嵌的硬核DSP单元来实现。

3.booth算法

看了原文献，有基2和基4两种实现

最常用的主要还是基2实现也就是用被除数的每两位做编码，Booth算法对乘数从低位开始判断，根据两个数据位的情况决定进行加法、减法还是仅仅移位操作。判断的两个数据位为当前位及其右边的位(初始时需要增加一个辅助位0)，移位操作是向右移动。

在Booth算法中，操作的方式取决于表达式(y【i+1】-y【i】)的值，这个表达式的值所代表的操作为：

0 无操作

+1 加x

-1 减x

Booth算法操作表示

yi yi+1 操作 说明

0 0 无 处于0串中，不需要操作

0 1 加x 1串的结尾

1 0 减x 1串的开始

1 1 无 处于1串中，不需要操作

乘法过程中，被乘数相对于乘积的左移操作可表示为乘以2，每次循环中的运算可表示为对于x(y(i+1)-yi)2^31-i项的加法运算(i=3l，30，…，1，0)。这样，Booth算法所计算的结果 可表示为：

x×(0-y31)×2^0

+x×(y31-y30)×2^1

+x×(y30-y29)×2^2

…

+x×(y1-y0)×2^31 [1] 

=x×(-y0×2^31 +y1×2^30 +y2×2^29+.......+y31×2^0)

=x×y

代码

module booth( start_sig, a, b, done_sig , product)
wire [:] start_sig;
wire [:] a;
wire [:] b;
wire [:] product;
/********************************/
reg[:] i;
reg[:] ra;
reg[:] rs;
reg[:] rp;
reg[:] x;
reg isdone;
always @(posedge clk or negedge rst_n)
if(!rst_n)
begin
         i<='d0;
         ra<='d0;
         rs<='d0;
         rp<='d0;
         x<='d0;
         isdone<='b0;
end
else if(start_sig)
        case(i)
        :
           begin
                ra<=a;
                rs<=(~a+);
                rp<={'d0,b,1'b0};
                i<=i+;
            end
        :
           if(x==)
                  begin
                       x<='d0;
                        i<=i+;
                  end
            else if(rp[:]=='b01)
                  begin
                        rp<={rp[:]+ra,rp[:]};
                         i<=i+;
                  end
           else if(rp[:]=='b10)
                  begin
                         rp<={rp[:]+rs,rp[:]};
                         i<=i+;
                  end
           else
                  i<=i+;
        :
            begin
                  rp<={rp[],rp[:]};
                  x<=x+;//返回去检测对应寄存器值的方法
                  i<=i-;
            end
        :
            begin
                  isdone<='b1;
                  i<=i+;
             end
        :
             begin
                  isdone<='b0;
                  i<='d0;
             end
        endcase
assign product=rp[:];
assign done_sig=isdone;
endmodule

例1.38　设被乘数M=0111(7),乘数Q=1101（－3），相乘过程如下：A为开始补加的零，

A 　       Q　Q－1

0000　1101　0　初始值

1001　1101　0　A=A－M=0000-0111=1001

1100　11　1　右移（第1次循环）/2

0011　1110　1　A=A + M=1100+0111=0011

0001　1111　0　右移（第2次循环）/2

1010　1111　0　A=A－M=0001-0111=1010

1101　0111　1　右移（第3次循环）/2

1110　1011　1　右移（第4次循环）/2

乘积=11101011=(-21)(十进制)

其中的移位是算数移位.

被乘数n位要移位3次.