WebGL编程指南案例解析之绘制四边形
//案例4,绘制矩形,和三角形类似,但是注意因为一个矩形有4个顶点,按照两个三角形绘制矩形的话,顶点顺序要注意 var vShader = `
attribute vec4 a_Position;
void main(){
gl_Position = a_Position;
}
`;
var fShader = `
void main(){
gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);
}
`; function main(){
//获取canvas元素
var canvas = document.getElementById('webgl'); //获取webgl上下文
var gl = getWebGLContext(canvas); if(!gl){
console.log('Failed to get the rendering context for WebGL!');
return;
} //初始化着色器
if(!initShaders(gl,vShader,fShader)){
console.log('Failed to initialize shaders.');
return;
} var n = initVertexBuffers(gl);
if(n < ){
console.log('Failed to set the positions of the vertices!');
return;
} //用指定颜色填充webgl容器,就是设置背景
gl.clearColor(0.4, 0.5, 0.0, 1.0);
gl.clear(gl.COLOR_BUFFER_BIT); gl.drawArrays(gl.TRIANGLE_STRIP,,n); function initVertexBuffers(gl){
//四个顶点
var vertices = new Float32Array([
-0.5,0.5,-0.5,-0.5,0.5,0.5,0.5,-0.5
]);
var n = ;//点的个数 //创建缓冲区对象
var vertexBuffer = gl.createBuffer();
if(!vertexBuffer){
console.log('Failed to create the buffer object!');
return -;
} //将缓冲区对象绑定到目标ARRAY_BUFFER
gl.bindBuffer(gl.ARRAY_BUFFER,vertexBuffer);
//往ARRAY_BUFFER
gl.bufferData(gl.ARRAY_BUFFER,vertices,gl.STATIC_DRAW); //获取shaderProgram中attribute变量‘a_Position’的地址
var a_Position = gl.getAttribLocation(gl.program,'a_Position');
if (a_Position < ) {
console.log('Failed to get the storage location of a_Position');
return -;
}
//将缓冲区对象分配给a_Position变量
gl.vertexAttribPointer(a_Position,,gl.FLOAT,false,,);
//开启着色器对缓冲区数据的访问
gl.enableVertexAttribArray(a_Position);
return n;
}
} main();
红字地方是相较绘制三角形作更改的。
另外,4个顶点的顺序,如下所示,有讲究的:
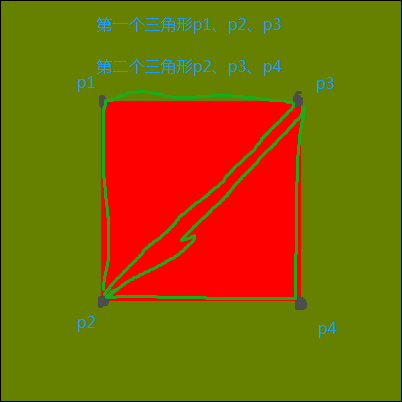
所以点坐标顺序为p1、p2、p3、p4.
其他绘制API(你可以根据如下API绘制你想要的图形):


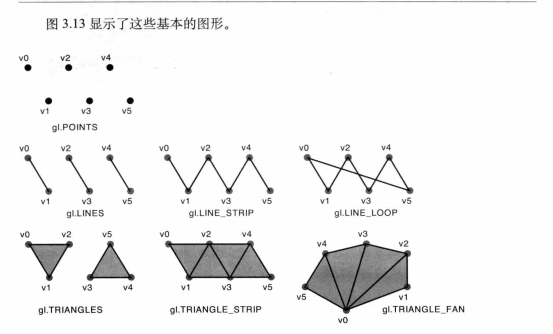
WebGL编程指南案例解析之绘制四边形的更多相关文章
- WebGL编程指南案例解析之绘制一个点
<!DOCTYPE html> <html> <head> <title>webgl</title> <style type=&quo ...
- WebGL编程指南案例解析之绘制三个点
//案例2.绘制3个点,将顶点数据存到缓冲区对象(gl.ARRAY_BUFFER)中,然后顶点着色器从里面读数据(3个顶点) //着色器将对这些顶点进行逐个解析, //第一个顶点给到顶点着色器,赋值给 ...
- WebGL编程指南案例解析之绘制三角形
//案例3.绘制三角形,将顶点数据存到缓冲区对象(gl.ARRAY_BUFFER)中,然后顶点着色器从里面读数据(3个顶点) //顶点着色器中去掉gl_PointSize = 10.0,绘制三角不能设 ...
- WebGL编程指南案例解析之平移和旋转的矩阵实现
手写各种矩阵: //矩阵 var vShader = ` attribute vec4 a_Position; uniform mat4 u_xformMatrix; void main(){ gl_ ...
- WebGL编程指南案例解析之3D视图视区问题
var VSHADER_SOURCE = 'attribute vec4 a_Position;\n' + 'attribute vec4 a_Color;\n' + 'uniform mat4 u_ ...
- WebGL编程指南案例解析之平移和旋转的math库实现
这里说的math库实现,指的是,通过一般的加减乘除(角度计算)来更新坐标值. 因为涉及到坐标的变化,所以这里都是基于对顶点着色器的修改 平移: var vShader = ` attribute ve ...
- WebGL编程指南案例解析之纹理叠加
var vShader = ` attribute vec4 a_Position; attribute vec2 a_TexCoord; varying vec2 v_TexCoord; void ...
- WebGL编程指南案例解析之加载纹理(贴图)
var vShader = ` attribute vec4 a_Position; attribute vec2 a_TexCoord; varying vec2 v_TexCoord; void ...
- WebGL编程指南案例解析之多数据存储于一个缓冲区以及着色器通信
//顶点着色器往片元着色器传值 //多个参数值存于一个缓冲对象中 var vShader = ` attribute vec4 a_Position; attribute float a_PointS ...
随机推荐
- mysql 出现的错误
1:创建函数时提示:This function has none of DETERMINISTIC, NO SQL, or READS SQL DATA ,因为当开启log-bin时,函数必须有参数, ...
- 前端基础(JavaScript)2
3.2 Array对象 3.2.1 数组创建 创建数组的三种方式: 创建方式1: var arrname = [元素0,元素1,….]; // var arr=[1,2,3]; 创建方式2: var ...
- redis—Spring中redis缓存的简单使用
这里使用的是 Spring-4.3 , redis-2.8 的版本 1.添加maven依赖 <dependency> <groupId>redis.clients</ ...
- Ubuntu下常用强化学习实验环境搭建(MuJoCo, OpenAI Gym, rllab, DeepMind Lab, TORCS, PySC2)
http://lib.csdn.net/article/aimachinelearning/68113 原文地址:http://blog.csdn.net/jinzhuojun/article/det ...
- lombok常见注解
一.使用lombok简化代码 lombok提供了很多注解,在编译时候生成java代码,代替了手工编写一些简单的代码,使程序员可以关注更重要的实现. 二.常用注解 以model为例 public cla ...
- SQL学习笔记之SQL查询练习题1
(网络搜集) 0x00 表名和字段 –1.学生表 Student(s_id,s_name,s_birth,s_sex) –学生编号,学生姓名, 出生年月,学生性别 –2.课程表 Course(c_id ...
- A8逻辑篇1.点亮一个LED(S5PV210.A8)
一.虚拟机安装好后,我们用Fedora 双击.vmx文件,将会在虚拟机中打开 相应的生成: 这些文件 二.进入虚拟机页面 等待启动 账号选择其他 用户名:root 密码:111111 设置页面大小: ...
- JVM的反射实现
java的反射机制 java的反射机制是在运行状态中,对于任意一个类(Class)都能知道他的属性(Field)和方法(Method),对于任意一个对象都能够调用它的方法和属性:这种动态获取信息以及动 ...
- 分布式Redis主备复制
当数据落在不同节点上时,如何保证数据节点之间的一致性是非常关键的 Redis采用主备复制的方式保证一致性,所有节点中,只有一个节点为主节点(master),它对外提供写服务,然后异步的将数据复制到其他 ...
- PowerDesigner16工具学习笔记-建立BPM
根据不同用途,BPM分为分析性(Analysis).执行型(Executable)和协作型(Collaborative) BPM的类型 业务流程语言 描述 分析型 Analysis 提供流程层次 ...
