BZOJ1001 [BeiJing2006]狼抓兔子 最小割 对偶图 最短路

原文链接http://www.cnblogs.com/zhouzhendong/p/8686871.html

题目传送门 - BZOJ1001

题意

　　长成上面那样的网格图求最小割。

　　$n,m\leq 1000$

题解

　　网格图先转个对偶图，然后SPFA跑一发就完事了。

　　或者你可以这样理解。

　　

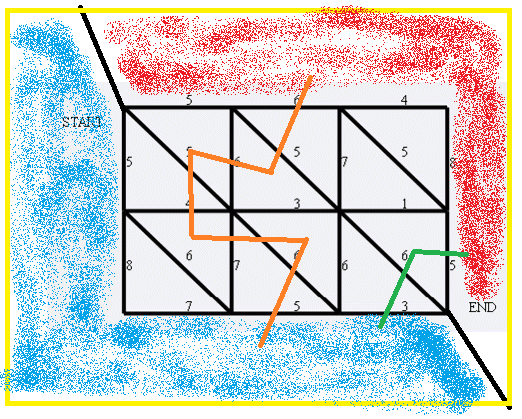
　　你要从红色区域到蓝色区域连一条路径，比如橙色或者绿色。

　　（其中绿色就是答案）

　　然后话费就是经过的边权值和。

　　然后你会发现消耗一条边的权值所达到的效果是沟通那条边所分割的两个区域。于是发现，以空白区域为节点，原图的边为边，最短路就是答案。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=2000005,M=1005;
struct Gragh{
	int cnt,y[N*3],z[N*3],nxt[N*3],fst[N];
	void clear(){
		cnt=0;
		memset(fst,0,sizeof fst);
	}
	void add(int a,int b,int c){
		y[++cnt]=b,z[cnt]=c,nxt[cnt]=fst[a],fst[a]=cnt;
	}
}g;
int n,m,nm,S,T;
void build(){
	int x,a,b;
	g.clear();
	for (int i=1;i<=n;i++)
		for (int j=1;j<m;j++){
			scanf("%d",&x);
			a=i==1?S:((i-2)*(m-1)+j);
			b=i==n?T:((i-1)*(m-1)+j+nm);
			g.add(a,b,x),g.add(b,a,x);
		}
	for (int i=1;i<n;i++)
		for (int j=1;j<=m;j++){
			scanf("%d",&x);
			a=j==m?S:((i-1)*(m-1)+j);
			b=j==1?T:((i-1)*(m-1)+j-1+nm);
			g.add(a,b,x),g.add(b,a,x);
		}
	for (int i=1;i<n;i++)
		for (int j=1;j<m;j++){
			scanf("%d",&x);
			a=(i-1)*(m-1)+j;
			b=(i-1)*(m-1)+j+nm;
			g.add(a,b,x),g.add(b,a,x);
		}
}
int vis[N],d[N],q[N],head,tail;
int SPFA(int S,int T){
	int n=T,qmod=n+1,x,y;
	head=tail=0;
	memset(d,63,sizeof d);
	memset(vis,0,sizeof vis);
	d[S]=0,vis[S]=1,q[++tail]=S;
	while (head!=tail){
		vis[x=q[head=(head+1)%qmod]]=0;
		for (int i=g.fst[x];i;i=g.nxt[i]){
			y=g.y[i];
			if (d[y]>d[x]+g.z[i]){
				d[y]=d[x]+g.z[i];
				if (!vis[y])
					vis[q[tail=(tail+1)%qmod]=y]=1;
			}
		}
	}
	return d[T];
}
int main(){
	scanf("%d%d",&n,&m),nm=(n-1)*(m-1);
	S=2*nm+1,T=S+1;
	build();
	printf("%d",SPFA(S,T));
	return 0;
}