[从今天开始修炼数据结构]图的最短路径 —— 迪杰斯特拉算法和弗洛伊德算法的详解与Java实现

在网图和非网图中，最短路径的含义不同。非网图中边上没有权值，所谓的最短路径，其实就是两顶点之间经过的边数最少的路径；而对于网图来说，最短路径，是指两顶点之间经过的边上权值之和最少的路径，我们称路径上第一个顶点是源点，最后一个顶点是终点。

我们讲解两种求最短路径的算法。第一种，从某个源点到其余各顶点的最短路径问题。

　　1，迪杰斯特拉(Dijkstra)算法

　　　　迪杰斯特拉算法是一个按路径长度递增的次序产生最短路径的算法，每次找到一个距离V0最短的点，不断将这个点的邻接点加入判断，更新新加入的点到V0的距离，然后再找到现在距离V0最短的点，循环之前的步骤。有些类似之前的普里姆算法，是针对点进行运算，贪心算法。

　　　　这里我们首先约定，Vi在vertex[]中存储的index = i，以方便阐述思路。思路如下：

　　　　（1）我们拿到网图，如下.我们要找到从V0到V8的最短路径，使用邻接矩阵存储的图结构。我们寻找距离V0最近的顶点，找到了邻接点V1，距离是1，将其连入最短路径。

　　

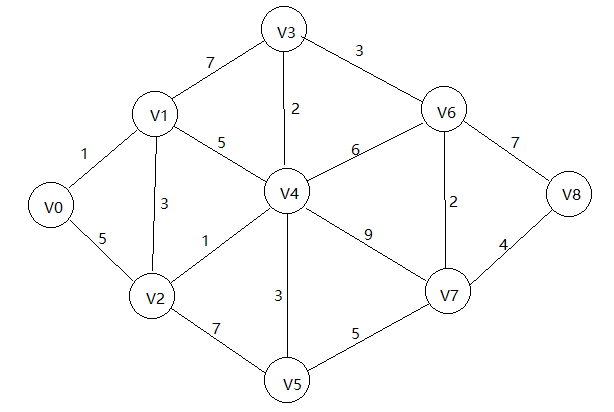
　　（2）修正与V1直接相关联的所有点到V0的最短路径。比如原本V2到V0的路径是5，现在通过V1，将其修改为1+3 = 4.，将V4置为6，V3置为8.我们现在就需要一个数组来存储每个点到V0的最短路径了。我们设置一个数组ShortPathTable[numVertex]来存储。

　　　　同时我们还需要存储每个点到V0的最短路径，为此我们设置一个数组Patharc[numVertex]，P[i] = k表示Vi到V0的最短路径中，Vi的前驱是Vk。我们还需要一个数组来存储某个顶点是否已经找到了到V0的最短路径，为此我们设置finals[numVertex]。此时

    S[] = { 0 , 1 , 4 , 8 , 6 , I , I , I , I }
    P[] = { 0 , 0 , 1 , 1 , 1 , 0 , 0 , 0 , 0 }
    f[] = { 1 , 1 , 0 , 0 , 0 , 0 , 0 , 0 , 0 }

　　（3）此时拿到与V0距离最短的点（还没有加入最短路径的，即final[i] = 0的点），这里是V2，然后更新V2的邻接点V4，V5到V0的最短路径分别为1+3+1=5和1+3+7=11，并将V2加入最短路径

    S[] = { 0 , 1 , 4 , 8 , 5 , I , I , I , I }
    P[] = { 0 , 0 , 1 , 1 , 2 , 0 , 0 , 0 , 0 }
    f[] = { 1 , 1 , 1 , 0 , 0 , 0 , 0 , 0 , 0 }

　　

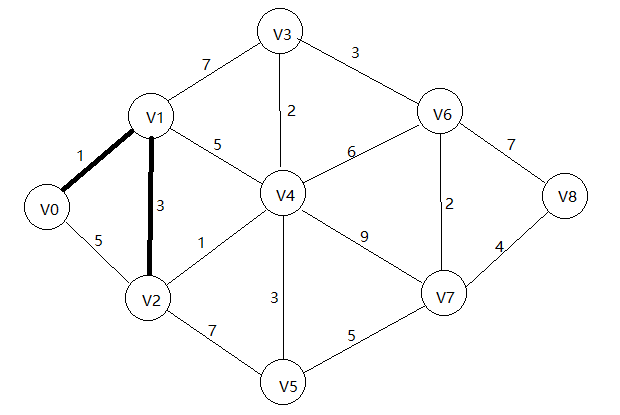
　　　　接下来的步骤跟前面类似，我就不再重复了，大家应该也理解迪杰斯特拉算法的步骤了，下面来看代码实现。

    public void ShortestPath_Dijkstra(){
        int[] ShortPathTable= new int[numVertex];
        int[] Patharc = new int[numVertex];
        int[] finals = new int[numVertex];

        //初始化
        for (int i = 0; i < numVertex; i++){
            ShortPathTable[i] = edges[0][i];    //初始化为v0的邻接边
            Patharc[i] = 0;
            finals[i] = 0;
        }
        finals[0] = 1;  //v0无需找自己的邻边

        int minIndex = 0;   //用来保存当前已经发现的点中到V0距离最短的点
        for (int i = 1; i < numVertex; i++){
            //找到目前距离V0最近的点
            int min = INFINITY;
            for (int index = 0; index < numVertex; index++){
                if (finals[index] != 1 && ShortPathTable[index] < min){
                    minIndex = index;
                    min = ShortPathTable[index];
                }
            }
            finals[minIndex] = 1;
            //更新还未加入最短路径的点到V0的距离
            for (int index = 0; index < numVertex; index++){
                if (finals[index] != 1 && (ShortPathTable[index] > (min + edges[minIndex][index]))){
                    ShortPathTable[index] = min + edges[minIndex][index];
                    Patharc[index] = minIndex;
                }
            }
        }
        //输出最短路径
        int s = 8;
        System.out.println(8);
        while ( s != 0){
            s = Patharc[s];
            System.out.println(s);
        }
    }

　　其实根据这个算法得到了v0到任意一个顶点的最短路径和路径长度的。时间复杂度O(n方)。

　　如果我们想得到v1，或者v2等到任意一个顶点的最短路径呢？我们要再跑一次这个算法才能得到这样复杂度就达到了O(n³)，这是我们所不能接受的。下面我们来介绍一种直接得到每一个顶点到另外一个顶点的最短路径。

　　2，弗洛伊德(Floyd)算法

　　　　弗洛伊德算法的想法是，如果V1到V2的距离，大于V1到V0再从V0到V2的距离，那么就把V1到V0的权值的拷贝，改为V1到V0+V0到V2. 同时把储存的最短路径也改掉，直到网中的每一条边都被遍历。

　　　　我们用二维矩阵ShortPathTable存储行号到列号的最短路径的权值之和（初始化为邻接矩阵）；Patharc存储行号到列号的最短路径中列号元素的前驱。初始化如下

　　　　举例如下：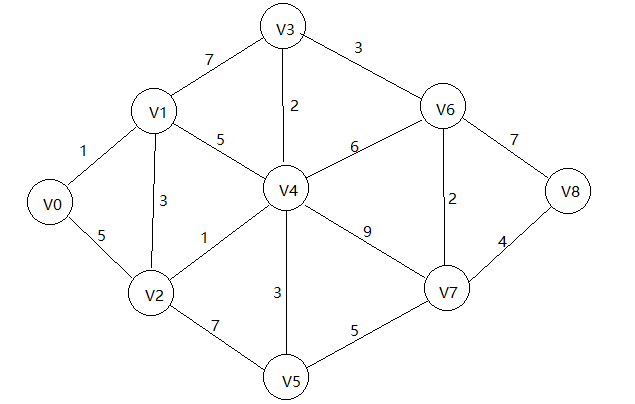

　　　　ShortPathTable矩阵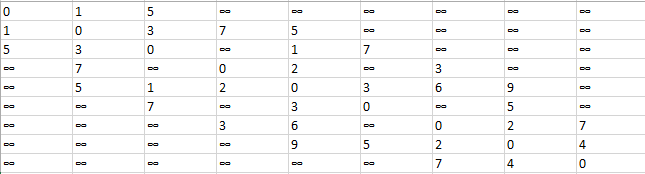： 　　Patharc矩阵：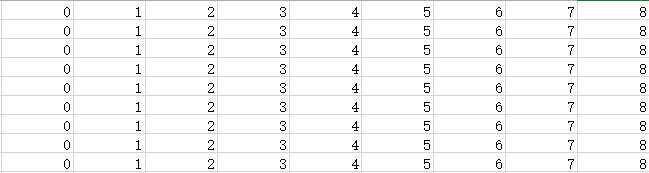

　　　　（1）从V0进入网图中，此时没有什么需要变化的。

　　　　 （2）到达V1，让所有的顶点的路径都从V1经过，发现V0到V2的路径大于先到V1再到V2的路径，所以将S矩阵和P矩阵中的相应位置更改。同理S[0][3] = 8, S[0][4] = 6。

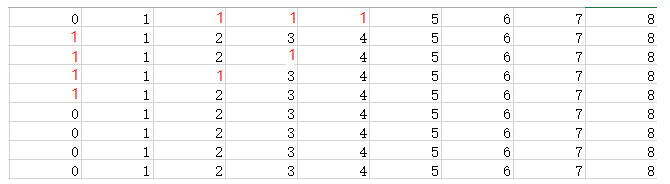
后面同理，依次循环V2~V8，针对每个顶点作为中转得到计算结果。这样我们的最短路径就完成了。

实现代码如下：

    public void ShortestPath_Floyd(){
        int[][] ShortPathTable = new int[numVertex][numVertex];
        int[][] Patharc = new int[numVertex][numVertex];
        //初始化两个矩阵
        for (int row = 0; row < numVertex; row++){
            for (int col = 0; col < numVertex; col++){
                ShortPathTable[row][col] = edges[row][col];
                Patharc[row][col] = col;
            }
        }

        for (int path = 0; path < numVertex; path++){
            for (int row = 0; row < numVertex; row++){
                for (int col = 0; col < numVertex; col++){
                    if (ShortPathTable[row][col] > (ShortPathTable[row][path] + ShortPathTable[path][col])){
                        ShortPathTable[row][col] = (ShortPathTable[row][path] + ShortPathTable[path][col]);
                        Patharc[row][col] = Patharc[row][path];
                    }
                }
            }
        }

        //打印看结果
        for (int row = 0; row < numVertex; row++) {
            for (int col = 0; col < numVertex; col++) {
                System.out.print(ShortPathTable[row][col] + "\t");
            }
            System.out.println();
        }
        System.out.println("***********************************");
        for (int row = 0; row < numVertex; row++) {
            for (int col = 0; col < numVertex; col++) {
                System.out.print(Patharc[row][col] + "\t");
            }
            System.out.println();
        }
    }

结果：

0    1    4    7    5    8    10    12    16
1    0    3    6    4    7    9     11    15
4    3    0    3    1    4    6     8    12
7    6    3    0    2    5    3     5    9
5    4    1    2    0    3    5     7    11
8    7    4    5    3    0    7     5    9
10   9    6    3    5    7    0     2    6
12   11   8    5    7    5    2     0    4
16   15   12   9    11   9    6     4    0
***********************************
0    1    1    1    1    1    1    1    1
0    1    2    2    2    2    2    2    2
1    1    2    4    4    4    4    4    4
4    4    4    3    4    4    6    6    6
2    2    2    3    4    5    3    3    3
4    4    4    4    4    5    7    7    7
3    3    3    3    3    7    6    7    7
6    6    6    6    6    5    6    7    8
7    7    7    7    7    7    7    7    8    

我们可以发现，P矩阵的第一列与迪杰斯特拉算法的结果是一样的。它的时间复杂度是三次方的，但它可以解决多个顶点到多个顶点的最短路径问题，比同样场景下的迪杰斯特拉算法要省时得多。

上面是两个算法对于无向图的应用，实际上对于有向图，也是同样的使用效果。因为无向图和有向图的区别仅仅是邻接矩阵是否对称而已。