深度学习面试题07：sigmod交叉熵、softmax交叉熵

目录

　　sigmod交叉熵

　　Softmax转换

　　Softmax交叉熵

　　参考资料

---

sigmod交叉熵

Sigmod交叉熵实际就是我们所说的对数损失，它是针对二分类任务的损失函数，在神经网络中，一般输出层只有一个结点。

假设y为样本标签，_y为全连接网络的输出层的值，那么，这个对数损失定义为

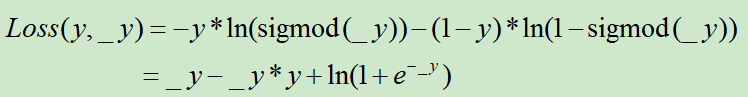
PS：这个是可以用极大似然估计推导出来的

举例：

y=0，_y=0.8，那此时的sigmod交叉熵为1.171

import numpy as np
def sigmod(x):
    return 1/(1+np.exp(-x))
y=0
_y=0.8
-y*np.log(sigmod(_y))-(1-y)*np.log(1-sigmod(_y))
#_y-_y*y+np.log(1+np.exp(-_y))

返回目录

Softmax转换

假设向量x=(x₁,x₂,...,x_m)，对x进行softmax转换的处理方式为：

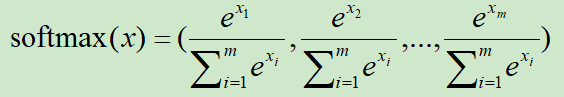
显然，x进行softmax处理后，会归一化为[0,1]，且和为1

举例：假设x=[0,2,-3],   softmax(x)=[0.11849965, 0.8756006 , 0.00589975]

 

返回目录

Softmax交叉熵

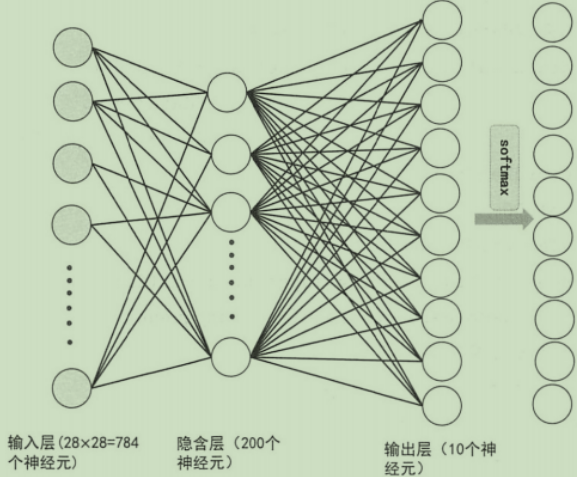
在神经网络的多分类中，假设是3分类，那么输出层就有3个神经元。

假设神经网络对某个样本的输出为out = [4,-5,6]，样本的真实标签为[0,0,1]，此时的softmax交叉熵为0.1269,计算公式为：

①首先对[4,-5,6]做softmax转换，softmax(out)=[1.19201168e-01  1.47105928e-05  8.80784121e-01]

②sum(-y*log(softmax(_y)))

import numpy as np
out = np.array([4,-5,6])
y = np.array([0,0,1])
softmax = np.exp(out)/sum(np.exp(out))
sum(-y*np.log(softmax))

Demo2：

import numpy as np
import tensorflow as tf

# 方式1
out = np.array([[4.0, -5.0, 10.0], [1.0, 5.0, 4.0], [1.0, 15.0, 4.0]],dtype=np.float64)
y = np.array([[0, 0, 1], [0, 1, 0], [0, 1, 0]],dtype=np.float64)
softmax = np.exp(out) /np.sum(np.exp(out),axis=1).reshape(-1,1)
res = np.sum(-y * np.log(softmax))/len(y)
print(res)

# 方式2
res2 = tf.losses.softmax_cross_entropy(onehot_labels=y, logits=out, label_smoothing=0)
print(tf.Session().run(res2))

# 方式3
res3 = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels=y,logits=out))
print(tf.Session().run(res3))
0.10968538820896588
0.10968538373708725
0.10968538820896594

返回目录

参考资料

《图解深度学习与神经网络：从张量到TensorFlow实现》_张平