2.2 convex hull凸包

1.定义：一组平面上的点，求一个包含所有点的最小的凸多边形，就是凸包问题。

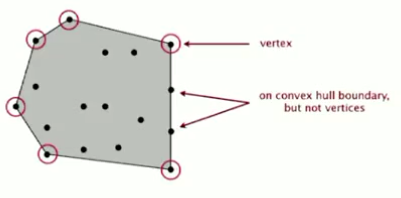
利用编程解决凸包问题，应该得到一组逆时针的顶点的顺序集合，在边上但不是顶点，则不包含在集合里。

2.机械的方法：将点所在的位置钉上钉子，用绳子围一圈，即得到凸包。但是无法进行编程。

3.假定2个几何前提：

（1）只能通过逆时针的方式来穿过凸包

（2）若选择y轴上坐标最小的点（最低点）为p，其他点到p的极角，按升序排列来编号

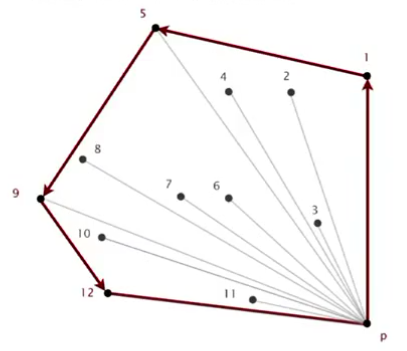
4.基于上面的两点事实，有一种Graham scan方法

（1）选择y最小的点为P

（2）使用点到P的极角对其他点进行排序（升序）

（3）依次考虑点，舍去那些无法产生逆时针旋转的点

例如：0-1-2-3-4，不是逆时针，且为了保证凸包，舍去3

0-1-2-4，同理，舍去2

0-1-4-5，舍去4

0-1-5-。。。。按照这个方法继续下去

5.一些挑战

（1）如何找到点P,即y值最小的点？

（2）如何按照极角对点进行排序？

这表明有时候需要能对相同的对象进行不同方式的排序

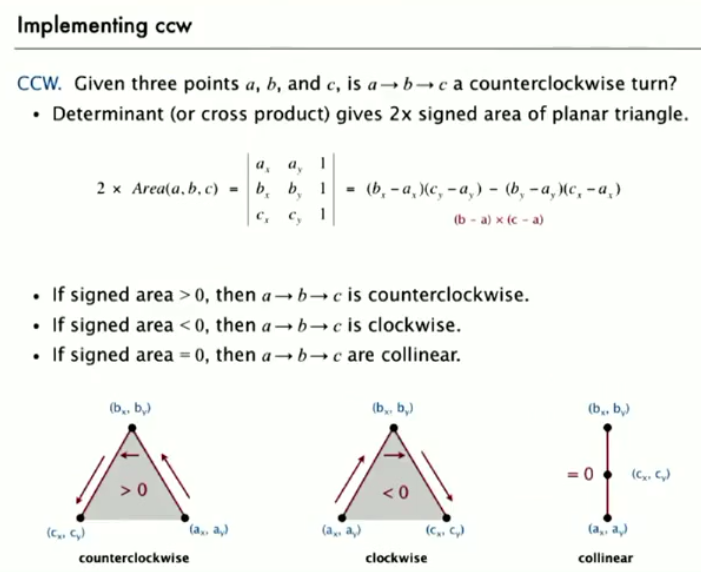
（3）如何判断p1-p2-p3是逆时针的顺序？

（4）如何有效的进行排序？  mergesort in NlogN

（5）如何解决几个点在一条线上的问题？

6.实现逆时针旋转

（1）理论基础：

（2）代码实现